Buna göre Δ − □ 'nin sonucu nedir?

Eğitim ve Öğretim Matematik
1

görüntü
görüntü2160×3840 3.55 MB

Buna göre \Delta - \square nin sonucu nedir *
I. \frac{\Delta}{\square} = \frac{3}{2}
II. \Delta+ \square = 15
III. \Delta - \square = ?
Yukarıdaki eşitliklerde \Delta ve \square sembolleri belli bir sayının yerine kullanılmıştır.

O 2
O 3
O 4
O 5
O 6

Açıklama: Metin bir matematik sorusu içermektedir. İlk metin belirli semboller (\Delta ve \square) ile ifade edilen matematiksel ifadeleri çözmeye yöneliktir.

2

Problemin Çözümü

Verilen ifadeleri değerlendirelim:

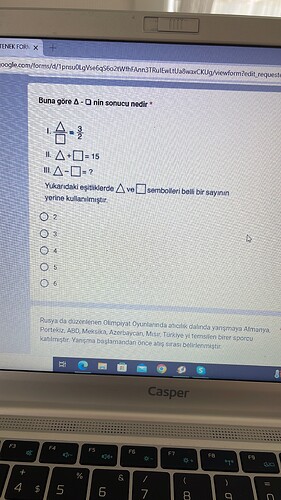
I. İfade: \frac{\Delta}{\square} = \frac{3}{2}

Bu ifadeyi yeniden düzenlersek:

\Delta = \frac{3}{2} \times \square

II. İfade: \Delta + \square = 15

Buradan \Delta'yı bulmak için yukarıdaki I. ifadeyi kullanarak yerine koyabiliriz. Elde edilen \Delta değerini kullanarak yeni bir denklem oluşturabiliriz.

III. İfade: \Delta - \square = ?

Bu ifade ise doğrudan sonuçlanmamaktadır. Ancak \Delta ve \square değerlerini bulduktan sonra bu işlemi yapabiliriz.

Sonuç için Değişkenleri Bulma

Şimdi yukarıdaki iki ifadeyi kullanarak belirsiz değişkenleri bulalım.

\Delta ve \square değerlerinin hesaplanması

Önce I. ifadede \Delta'yı bulalım:

Denklem:

\Delta = \frac{3}{2} \times \square

Bu ifadeyi II. ifadeye yerleştirebiliriz:

\frac{3}{2} \times \square + \square = 15

Buradan \square için ortak çarpanı alalım:

\left(\frac{3}{2} + 1\right) \square = 15

1 ifadesini \frac{2}{2} ile eşdeğer hale getirirsek:

\left(\frac{3}{2} + \frac{2}{2}\right) \square = 15

Burası:

\frac{5}{2} \square = 15

Her iki tarafı \frac{2}{5} ile çarparak \square'yı bulabiliriz:

\square = 15 \times \frac{2}{5} = 6

Bunu \square'ın değerini kullanarak \Delta'yı bulalım:

\Delta = \frac{3}{2} \times 6 = 9

\Delta - \square işlemi

Artık her iki sembolün değerini biliyoruz:

  • \Delta = 9
  • \square = 6

Bunları yerine koyduğumuzda:

\Delta - \square = 9 - 6 = 3

Bu durumda doğru cevap 3’tür.

Cevap

3

TERİMLER:

Sembol: Matematiksel ifadelerde belirli sayıları temsil etmek için kullanılan işaretlerdir. Örneğin \Delta ve \square burada birer semboldür.