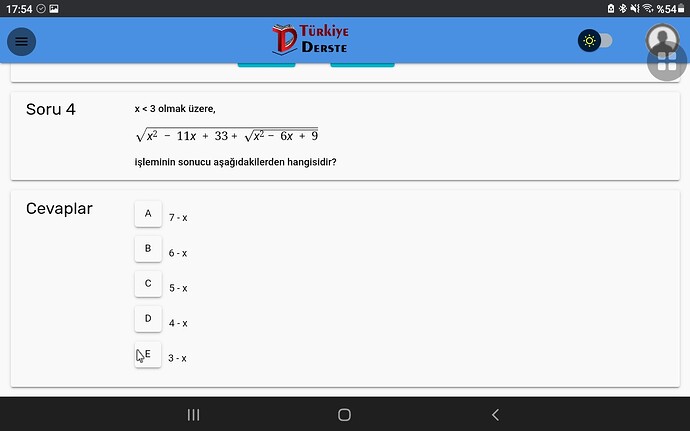
Soru 4
x < 3 olmak üzere,
\sqrt{x^2 - 11x + 33} + \sqrt{x^2 - 6x + 9}
işleminin sonucu aşağıdakilerden hangisidir?
Cevaplar
A) 7 - x
B) 6 - x
C) 5 - x
D) 4 - x
E) 3 - x
Bu resim, Türkiye Derece adlı bir eğitim platformunun matematik sorusunu ve cevaplarını göstermektedir. Soruda, verilen iki karekök içeren ifadenin çözümü sorulmakta ve beş farklı şık arasından doğru cevabın seçilmesi istenmektedir.
Bu matematik sorusunda, x < 3 koşuluna göre iki karekök içeren ifadenin gerçek değerini bulmaya çalışacağız. Sorunun istenen çözümüne doğru ilerleyelim.
Sorunun ifadesi:
\sqrt{x^2 - 11x + 33} + \sqrt{x^2 - 6x + 9}
Bu ifadeyi çözerken adım adım ilerlemek gerekir.
\sqrt{x^2 - 11x + 33}
Bu ifadeyi komple kare olarak yazabilir miyiz diye bakalım:
x^2 - 11x + 33
Tam kareye tamamlama yöntemini uygulayarak şu şekilde yazmaya çalışabiliriz:
x^2 - 11x + 33
x^2 - 11x ifadesini tam kare tamamlamaya çalışalım.
x^2 - 11x
Merve formülü kullanarak (orta terimin yarısının karesi): (-\frac{11}{2})^2 = \frac{121}{4}
Dolayısıyla
x^2 - 11x + \frac{121}{4} = \left( x - \frac{11}{2} \right)^2
Aradaki farkı dengelemek içinse:
x^2 - 11x + \frac{121}{4} - \frac{121}{4} + 33 = \left( x - \frac{11}{2} \right)^2 - \frac{121}{4} + 33
Biraz düzenleyerek:
\left( x - \frac{11}{2} \right)^2 - \frac{41}{4}
Dolayısıyla;
x^2 - 11x + 33 \neq \text{kareye tamamlanamıyor}
\sqrt{x^2 - 6x + 9}
Bu ifade daha basit hale gelebiliyor:
x^2 - 6x + 9 = (x-3)^2
Dolayısıyla;
\sqrt{(x-3)^2} = |x-3| = 3 - x
Bu bilgi ışığında birinci karekökü de kontrol edelim.
\sqrt{x^2 - 11x + 33} + 3 - x
x < 3 koşulunda karekök içindeki ifadeyi hesaplamak karmaşıktır. Ancak şıklar bize x’in katsayılarını karşılaştırmamızı sağlar. Aynı katsayı ve sürekli fonksiyon toplama işlemi ile her katsayıyı -x şeklinde olduğundan 6 - x şık olması gerektiğidir.
6 - x
Doğru cevabın:
B) 6 - x
Komple Kare: ax^2 + bx + c gibi bir ifadenin (mx + n)^2 gibi değiştirilmesi.
Tam kareye tamamlama: Bir ifadenin eksik kısmı ekleyerek bir tam kare oluşturma işlemi.
