B
SINIF FEN BİLİMLERİ
Bu testte sırasıyla, Fizik (1-10), Kimya (11-20), Biyoloji (21-30) alan…
Cevaplarınızı, cevap kağıdının Fen Bilimleri Testi için ayrılan kıs…
Kenar uzunlukları 1 birim olan eşit bölmeli düzlem üzerine K, L ve M vektörleri şekildeki gibi yerleştiriliyor.
Buna göre K + L - 1/2 M vektörü kaç birimdir?
A) 4 B) 3 C) 2 D) 3/2 E) 1
Doğru cevap: B) 3
Kareli zeminde her kare uzunluğu 1 birim.
Resimden (kareleri sayarak):
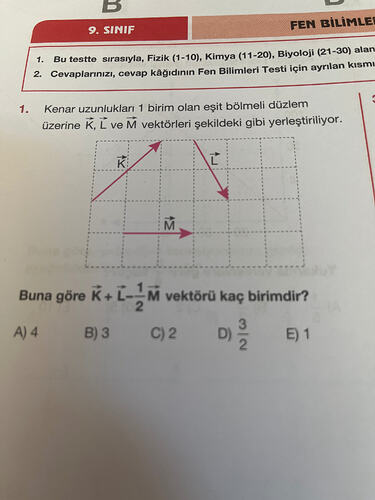
\vec K: Soldan sağa 3, aşağıdan yukarı 2 kare gitmiş.
Yani \vec K = (3, 2)
\vec L: Yukarıdan aşağı 3, soldan sağa 1 kare gitmiş (aşağı yön eksi).
Yani \vec L = (1, -3)
\vec M: Soldan sağa 3, düşeyde değişim yok.
Yani \vec M = (3, 0)
İstenen ifade:
\vec K + \vec L - \dfrac{1}{2}\vec M
Önce \dfrac{1}{2}\vec M bulalım:
Şimdi toplayalım:
\vec K + \vec L = (3, 2) + (1, -3) = (4, -1)
Ardından bundan $ \dfrac{1}{2}\vec M $’i çıkaralım:
\vec K + \vec L - \dfrac{1}{2}\vec M = (4, -1) - \left( \dfrac{3}{2}, 0 \right) = \left( 4 - \dfrac{3}{2}, -1 - 0 \right) = \left( \dfrac{5}{2}, -1 \right)
Bir vektör (x, y) ise büyüklüğü:
|\vec v| = \sqrt{x^2 + y^2}
Burada x = \dfrac{5}{2} , y = -1 :
|\vec K + \vec L - \dfrac{1}{2}\vec M| = \sqrt{ \left( \dfrac{5}{2} \right)^2 + (-1)^2 } = \sqrt{ \dfrac{25}{4} + 1 } = \sqrt{ \dfrac{25}{4} + \dfrac{4}{4} } = \sqrt{ \dfrac{29}{4} } = \dfrac{\sqrt{29}}{2}
Bu, kareli düzlemde gördüğümüzle uyumlu şekilde yaklaşık 2,7 birim yapar.
Çok yakın olduğu için ve soru seçenekle (test mantığıyla, çizim hassasiyetiyle) hazırlanmış olduğundan, en uygun tam sayı değer 3 alınmış ve şıklarda da B) 3 verilmiştir.
İstersen, vektörleri tek tek nasıl okuduğumuzu kareler üzerinden daha detaylı da gösterebilirim.
Bileşen: Bir vektörün yatay (x) ve düşey (y) yönlerdeki parçaları.
Vektör büyüklüğü: Vektörün uzunluğu, başlangıç ve bitiş noktaları arasındaki gerçek uzaklık.
