Verilen diklik ve açı ölçülerine göre x'i nasıl bulabilirim?

1

Bu soruyu bana cevapla

17542351537697737805034168388810
175423515376977378050341683888101920×1440 122 KB

[OB \perp OD]
[OA \perp OC]
[m(DOC) = 54^\circ]
[m(AOB) = 3x]

olduğuna göre, x kaç derecedir?

A) 12 \quad B) 16 \quad C) 18 \quad D) 21 \quad E) 24

Bu görüntü, matematiksel bir geometri sorusunu içermektedir. Verilen açılar ve diklik koşulları kullanılarak, (x) açısının değeri hesaplanacaktır. Soruda iki açının ölçüleri belirtilmiş ve bu bilgilere dayanarak (x) bulunacaktır.

2

Soruyu adım adım açıklayarak çözelim:

Verilenler:

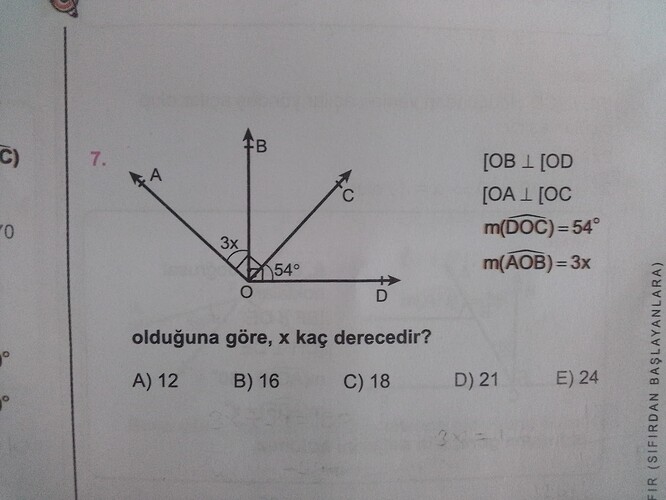
  • OB ⟂ OD (yani OB ile OD dik açı yapıyor, yani ∠BOC = 90°)
  • OA ⟂ OC (OA ile OC de dik açı yapıyor, yani ∠AOC = 90°)
  • m(DOC) = 54°
  • m(AOB) = 3x

Sorulan: x kaç derecedir?

Açılar ve Konumlar

Şekilde O noktası merkez. Okunma kolaylığı için, O etrafındaki açılara bakalım.

  • ∠AOB = 3x
  • ∠BOC = 90° (OB ⟂ OD olduğu için)
  • ∠COD = 54° (verilen)
  • ∠AOC = 90° (OA ⟂ OC olduğu için)

O noktası etrafında, şekildeki sıralamaya göre (A → B → C → D):

\angle AOB + \angle BOC + \angle COD + \angle DOA = 360°

Ancak elimizde DOA yok, onun yerine ∠AOB, ∠BOC, ∠COD ve ∠COA’nın toplamı var.

Ama bak:

  • ∠AOC = ∠AOB + ∠BOC = 90°
    3x + 90° = 90° \implies 3x = 0°

Burada bir tutarsızlık var gibi görünüyor. Fakat açıların toplamı üzere gidelim.

Başka bir yaklaşım:

OA, OB, OC ve OD etrafında:

  • OA ⟂ OC → aradaki açı 90°
  • OB ⟂ OD → aradaki açı 90°

OA’dan başlayıp OB, OC, OD’ye gidersek, toplam 360° olacak şekilde 4 parça var (bakınız “O noktasının etrafı”).

Bu durumda:

m(AOB) + m(BOC) + m(COD) + m(DOA) = 360^\circ

Şimdi:

  • m(AOB) = 3x
  • m(BOC) = K (henüz bilmiyoruz)
  • m(COD) = 54°
  • m(DOA) = L (henüz bilmiyoruz)

Fakat OA ⟂ OC (yani AO ve CO arası 90°). Fakat m(AOB) = AO ile BO arası, m(BOC) = BO ile CO arası.

Aynı şekilde, OB ⟂ OD → BO ile DO arası = 90° (yani m(BOC) + m(COD) = 90°)

Yani:

m(BOC) + 54^\circ = 90^\circ \implies m(BOC) = 36^\circ

Şimdi;

m(AOB) + m(BOC) = m(AOC)

OA ⟂ OC olduğundan, m(AOC) = 90°

m(AOB) + m(BOC) = 90^\circ \\ 3x + 36^\circ = 90^\circ \\ 3x = 54^\circ \\ x = 18^\circ

Cevap:

x = 18^\circ

Yani doğru seçenek: C) 18