Bu soruyu bana basitçe anlat
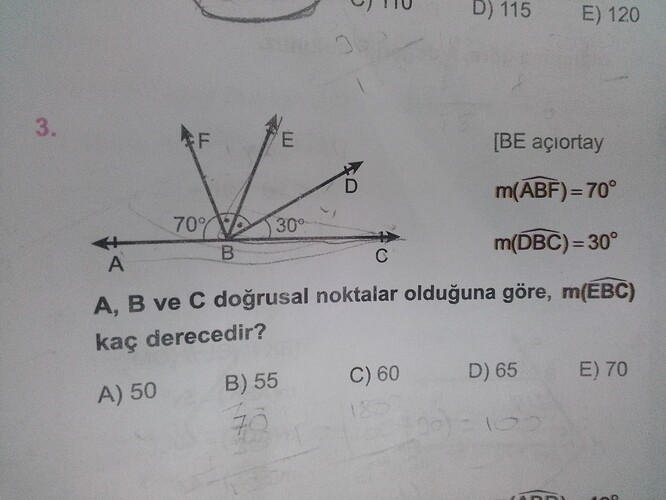
[BE açıortay
m(ABF) = 70^\circ
m(DBC) = 30^\circ
A, B ve C doğrusal noktalar olduğuna göre, m(EBC) kaç derecedir?
A) 50 B) 55 C) 60 D) 65 E) 70
Bu resim bir matematik sorusu içermektedir. Açı hesaplamasıyla ilgili bir problem sunulmuş ve verilen açıların yardımıyla istenen açının hesaplanması beklenmektedir. Bir doğru üzerindeki noktalar ve açıortay bilgisi verilerek, doğru cevabın seçilmesi isteniyor.
Soruyu adım adım ve basitçe açıklayayım:
Soru:
A, B ve C doğrusal noktalar.
m(ABF) = 70°, m(DBC) = 30°
[BE açıortay.
Soru: m(EBC) kaçtır?
Adımlar:
-
A, B, C doğrusal olduğu için, A ile C arası düz açı:
m(ABC) = 180°
-
m(ABF) = 70°
Yani F noktası, A ile B arasındaki çizgiden 70° ile yukarıda.
-
m(DBC) = 30°
Yani D noktası, B ile C arasındaki çizgiden 30° ile yukarıda.
-
Açıları bulalım:
m(FBD) = 180° - 70° - 30° = 80°
(Çünkü A’dan C’ye toplam açı 180°, iki dış açıyı çıkarıyoruz.)
-
BE açıortay olduğu için:
m(FBE) = m(EBD) olur.
m(FBD) = 80°
O hâlde:
m(FBE) = m(EBD) = \frac{80°}{2} = 40°
-
Bize sorulan:
m(EBC) yani E, B, C açısı:
m(EBC) = m(EBD) + m(DBC) = 40° + 30° = 70°
Cevap: 70°
Kısacası, açıortaydan dolayı 80°'yi ikiye böldük ➔ 40°
Sonra B, E, C açısı için 40° + 30° topladık ➔ 70°
Yani doğru cevap: E şıkkı, 70