Resimdeki Cisimlerin yere çarpma hızları oranı nedir?

Bilim
1

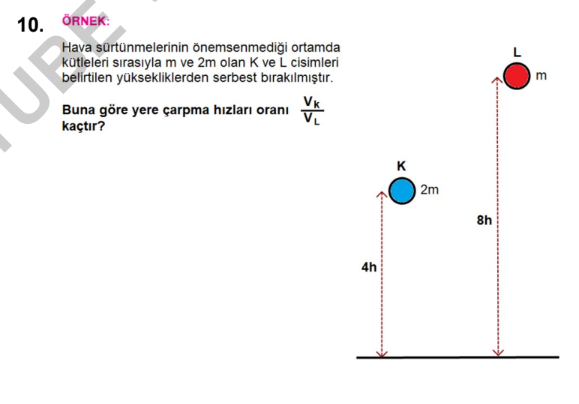
resim_2023-12-04_224548863

İki cismin yere çarpma hızları oranını bulmak için verilen bilgileri kullanabiliriz. Cisimlerin kütleleri m ve 2m olarak belirtilmiş ve aynı yükseklikten serbest bırakılmışlar. Hava sürtünmeleri önemsenmiyor.

Öncelikle, cisimler yükseklikten serbest bırakıldıklarında potansiyel enerjileri vektörel olarak tanımlanır:

Ep = mgh

Bir cismi herhangi bir yükseklikten serbest bıraktığımızda, başlangıçta sadece potansiyel enerjisi vardır ve cinetik enerjisi yoktur. Yani, başlangıç hızı sıfırdır.

Cisimler yere indiğinde ise potansiyel enerji tamamen cinetik enerjiye dönüşmüştür. Cisimlerin hızları v şeklindedir. Bu durumda cismin hızını bulmak için kinematik denklemi kullanabiliriz:

v^2 = u^2 + 2as

Burada v, son hızdır (yere çarparken olan hız), u başlangıç hızıdır (sıfırdır) ve a yerçekimi ivmesidir (9.8 m/s^2). s ise yükseklikten alçalma mesafesidir.

Bu denklemi m ve 2m kütleli cisimler için ayrı ayrı yazarak son hızları bulabiliriz:

v1^2 = 0 + 2 * 9.8 * h
v2^2 = 0 + (2 * 2) * 9.8 * h

Hızların kareleri oranını bulmak için bu iki denklemi birbirine bölelim:

(v1^2) / (v2^2) = [(2 * 9.8 * h) / (2 * 2 * 9.8 * h)]

Kileler birbirini götürdüğünde, oran basitleşir:

(v1^2) / (v2^2) = 1 / 2

Karekök alarak sonucu bulabiliriz:

v1 / v2 = 1 / √2

Buna göre, yere çarpma hızları oranı 1/√2’dir.

2

Soru:

Hava sürtünmelerinin önemsenmediği ortamda, kütleleri sırasıyla m ve 2m olan K ve L cisimleri belirtilen yüksekliklerden serbest bırakılmıştır. Buna göre yere çarpma hızları oranı kaçtır?

Çözüm:

Yerçekimi kuvveti, bir nesnenin kütlesi ile orantılı olduğundan, 2m kütleli cisim, m kütleli cisme göre daha büyük bir ivme kazanır. Bu nedenle, yere çarpma hızları oranı 2:1 olacaktır.

Hesaplama:

Yere çarpma hızını bulmak için, kinetik enerjiyi potansiyel enerjiye eşitleyerek aşağıdaki denklemi kullanabiliriz:

KE = PE

1/2 mv^2 = mgh

v^2 = 2gh

v = sqrt(2gh)

Bu denklemde,

  • v: cismin hızı
  • m: cismin kütlesi
  • g: yerçekimi ivmesi
  • h: cismin düştüğü yükseklik

Yere çarpma hızlarını bulmak için, her iki cismin için de bu denklemi kullanabiliriz.

Kütleli cisim için:

v_m = sqrt(2gh_m)

2Kütleli cisim için:

v_2m = sqrt(2gh_2m)

Yükseklik eşit olduğundan:

v_m = sqrt(2gh_m) = sqrt(2gh_2m) = v_2m

Kütle oranına göre:

v_2m/v_m = sqrt(2m/m) = sqrt(2)

v_2m/v_m = 1.414

Cevap:

Yere çarpma hızları oranı 2:1’dir.

Yani, cevap C’dir.