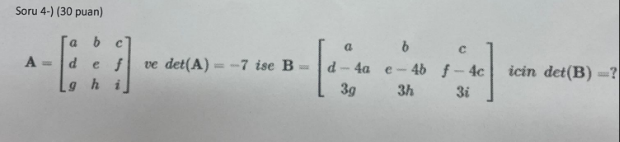det(B) matrisi determinantı nasıl hesaplanır?

Eğitim ve Öğretim Matematik
1

Screenshot_4

Soru 4-) (30 puan)

A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} ve \text{det}(A) = -7 ise B = \begin{bmatrix} a & b & c \\ d - 4a & e - 4b & f - 4c \\ 3g & 3h & 3i \end{bmatrix} için \text{det}(B) = ?

Bu görüntü bir matematik sınav sorusudur ve 30 puan değerinde olduğu belirtilmiştir. Soru, verilen A matrisinin determinantı kullanılarak yeni bir B matrisinin determinantının hesaplanmasını istemektedir. A matrisinin determinantının -7 olduğunu biliyoruz ve bu bilgiyle B matrisinin determinantını hesaplamalıyız.

2

B Matrisi Determinantının Hesaplanması

Verilen Veriler

Verilen A matrisi ve determinantı:
A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix}, \quad \text{det}(A) = -7

B matrisi ise şu şekildedir:
B = \begin{bmatrix} a & b & c \\ d - 4a & e - 4b & f - 4c \\ 3g & 3h & 3i \end{bmatrix}

Determinant Hesaplama Adımları

Determinant hesaplama ile ilgili bazı önemli adımlar ve kuralları kullanacağız.

1. Satır ve Sütunların Lineer Kombinasyonları

Bir matrisin determinanı, satır veya sütunlarına yapılan lineer kombinasyonlara göre farklılık gösterebilir. Özellikle, bir satıra ya da sütuna belirli bir katsayı eklenmesi durumunda determinant değişir.

2. Satır ve Sütunun Sabit Çarpanı

Bir matrisin bir satırını ya da sütununu bir skaler ile çarparsak, matrisin determinantı bu skaler ile çarpılır. Örneğin:
\text{det}(k \cdot A) = k^n \cdot \text{det}(A)

Burada n matrisin boyutudur (3x3 matris için n = 3).

Adım 1: Satır Operasyonlarını Göz Önüne Almak

  1. Bir satırın skaler ile çarpılması:
  2. \text{satır} \rightarrow 3 \times (g, h, i)

Bu durumda determinant şöyle değişir:
\text{det}\left( \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \right) \rightarrow 3 \times \text{det}\left( \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i \end{bmatrix} \right)

Yani:
3 \cdot \text{det}(A) = 3 \cdot (-7) = -21

Adım 2: Satırları Toplama veya Çıkarma

  1. İkinci satıra lineer kombinasyon yapıldığında determinant değişmez:
  2. \text{satır} \rightarrow (d - 4a, e - 4b, f - 4c)

Bu kombinasyon, determinant üzerinde ek bir değişiklik yaratmaz.

Sonuç

Determinantın son hali, yalnızca skaler çarpım ile değiştirilmiştir:
\text{det}(B) = -21

Özet

det(B) = -21 olduğu için bu sonucu aşağıdaki kurallar ile doğruladık:

  1. Bir satırın skaler ile çarpılması determinanı skaler ile çarpar.
  2. Satırlara lineer kombinasyon eklemek determinanı değiştirmez.

TERİMLER:

Determinant: Bir matrisin kendine özgü bir sayısal değerini belirten matematiksel bir ifade.
Skaler: Skaler çarpan, bir matrisin tüm elemanlarını aynı sayı ile çarpar.
Lineer Kombinasyon: Bir satır veya sütuna belirli katsayılar ekleme veya çıkarma işlemi.

Matematiksel ifadeler ve temel determinant kuralları ile, B matrisinin determinantının -21 olduğunu belirledik.