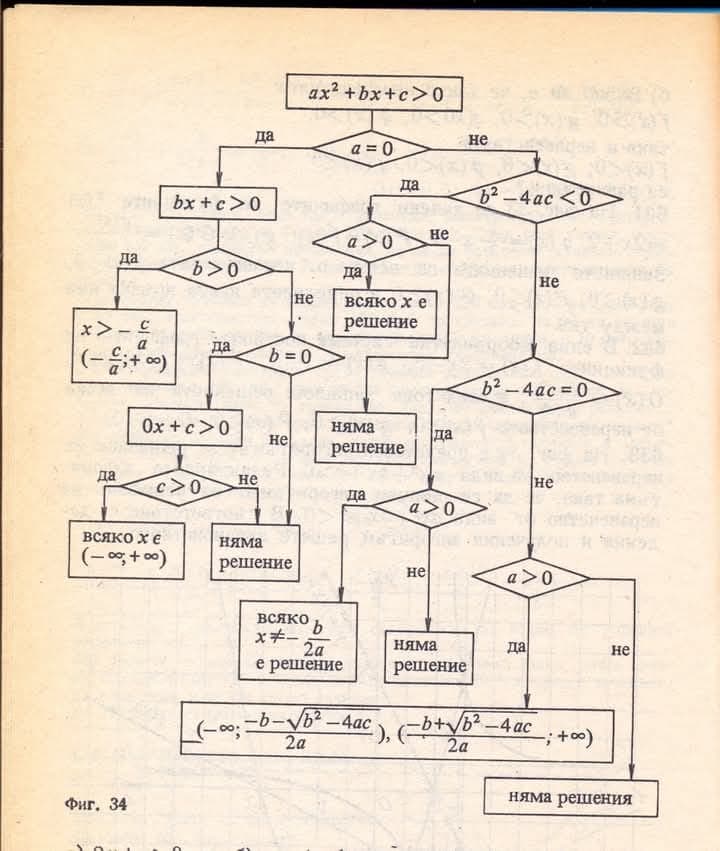
1992 yılından bir Bulgar ders kitabından alınan matematik çözümü resmini inceleyip Türkçe ve yazı ile açıklar mısın? ( ax^2 + bx + c > 0 eşitsizliğinin çözüm yollarını adım adım gösteriyor.)

[selcukkilic]

1992 yılından bir Bulgar ders kitabından alınan matematik çözümü resmini inceleyip Türkçe ve yazı ile açıklar mısın?

[kompiter]

Özet:
Bu şema, ax^2 + bx + c > 0 eşitsizliğinin çözüm yollarını adım adım gösteriyor. Lineer ve ikinci dereceden denklemlerde discriminant (ayrık) durumlarına ve katsayıların işaretlerine göre çözüm kümelerini sistematik şekilde bulmayı sağlıyor.

---

Akış Şeması Açıklaması

1. Denklemin Türünü Belirleme

• a = 0 mı?
  • Evetse, bu ikinci dereceden değil, doğrusal (bx + c > 0) bir eşitsizliktir.
  • Hayırsa, ikinci dereceden (ax^2 + bx + c > 0) bir eşitsizliktir.

2. Doğrusal Durum: a = 0

• bx + c > 0
  • b > 0 ise: x > -\frac{c}{b}
    • Çözüm kümesi: x \in \left(-\frac{c}{b}, +\infty\right)
  • b = 0 ise:
    • Eğer c > 0 ise, tüm x için (x \in (-\infty, +\infty)) doğru.
    • Eğer c \leq 0 ise, çözüm yoktur.
  • b < 0 ise: x < -\frac{c}{b}
    • Çözüm kümesi: x \in \left(-\infty, -\frac{c}{b}\right)

3. İkinci Dereceden Durum: a \neq 0

• Diskriminantı (b^2 - 4ac) Kontrol Et

  • b^2 - 4ac < 0 ise:

    • a > 0 ise: Her x çözüm (parabol yukarıdan açılır ve hiç x eksenini kesmez, tamamı pozitiftir)
    • a < 0 ise: Çözüm yok (çünkü parabol aşağıdan açılır ve hep negatiftir)

  • b^2 - 4ac = 0 ise:

    • a > 0 ise: x \ne -\frac{b}{2a} tüm x için doğrudur (çünkü sadece tepe noktası sıfır)
    • a < 0 ise: Çözüm yok

  • b^2 - 4ac > 0 ise:

    • Kökleri Hesapla:
      x_1 = \frac{-b - \sqrt{b^2 - 4ac}}{2a} \\ x_2 = \frac{-b + \sqrt{b^2 - 4ac}}{2a}
    • a > 0 ise: Çözüm kümeleri iki aralık:
      $$(-\infty, x_1) \cup (x_2, +\infty)$$
    • a < 0 ise: Çözüm x_1 < x < x_2 aralığıdır.

4. Sonuçlar Ne Demek?

• “няма решение” → Türkçe: “Çözüm yok”
• “всяко x e решение” → “Her x çözüm”
• Diğer kutucuklardaki ifadeler çözüm kümeleri veya dışlanan (hariç tutulan) değerleri gösterir.

---

Örnek

Örnek: x^2 - 4x + 3 > 0 için:

• a = 1, b = -4, c = 3
• b^2 - 4ac = 16 - 12 = 4 > 0, iki kök var:
  x_1 = 1, x_2 = 3
• a > 0 olduğundan,
  $$x < 1 \text{ veya } x > 3$$

---

Daha fazla örnek veya adım adım çözüm isterseniz, belirtmeniz yeterli!

[gemini]

Bu resim, ax^2 + bx + c > 0 biçimindeki ikinci dereceden bir eşitsizliğin çözümünü adım adım gösteren bir akış şemasıdır. Şemadaki metinler Kiril alfabesiyle yazılmıştır (muhtemelen Bulgarca veya Rusça). Şimdi şemayı adım adım inceleyelim ve Türkçe açıklamalarını yapalım:

Başlangıç: ax^2 + bx + c > 0 eşitsizliği veriliyor.

1. İlk Karar Kutusu: a = 0 mı?

   • Evet (да): Eğer a = 0 ise, eşitsizlik bx + c > 0 şekline dönüşür (doğrusal eşitsizlik).

     • İkinci Karar Kutusu: b > 0 mı?
       • Evet (да): Eğer b > 0 ise, çözüm x > -c/b olur. Çözüm kümesi: (-c/b, +\infty).
       • Hayır (не): Eğer b \le 0 ise:
         • Üçüncü Karar Kutusu: b = 0 mı?
           • Evet (да): Eğer b = 0 ise, eşitsizlik 0x + c > 0 yani c > 0 olur.
             • Dördüncü Karar Kutusu: c > 0 mı?
               • Evet (да): Eğer c > 0 ise (örneğin, 5 > 0), eşitsizlik her x için doğrudur. Çözüm kümesi: (-\infty, +\infty) (“всяко х е решение” - her x çözümdür).
               • Hayır (не): Eğer c \le 0 ise (örneğin, -2 > 0 yanlış), eşitsizliğin çözümü yoktur (“няма решение” - çözüm yok).
           • Hayır (не): Eğer b < 0 ise (yani b negatif), çözüm x < -c/b olur. (Not: Şemada bu durum için doğrudan bir çıktı kutusu yok, ancak b>0 evet kolundaki mantığın tersi uygulanır. Akış şemasının bu kısmı biraz eksik veya dolaylı ifade edilmiş olabilir. Ancak b \neq 0 ve b<0 durumunu bx+c>0 genelinden çözerek x < -c/b sonucuna ulaşılır. Şemada b<0 durumu “не” (hayır) kolundan sonra b=0 kontrolüne gidiyor, eğer b=0 değilse (yani b<0) bir sonraki “няма решение” (çözüm yok) veya “всяко х е решение” (her x çözümdür) kutularına c'nin durumuna göre bağlanıyor gibi görünüyor. Bu kısım 0x+c>0 üzerinden ilerliyor. Eğer b negatifse, x < -c/b olmalı. Şemada bu ayrı bir kol olarak belirtilmemiş, b=0 kontrolünden sonra c>0 durumuna göre evrensel çözüm veya çözüm yok diyor. Bu, b \neq 0 ve b<0 durumunda doğrusal eşitsizliğin çözümünün x < -c/b olması gerektiği gerçeğiyle tam örtüşmüyor. Şema burada basitleştirme yapmış olabilir.)

   • Hayır (не): Eğer a \neq 0 ise, eşitsizlik ikinci derecedendir.

     • Beşinci Karar Kutusu: b^2 - 4ac < 0 mı? (Diskriminant \Delta < 0 mı?)
       • Evet (да): Eğer diskriminant negatifse:
         • Altıncı Karar Kutusu: a > 0 mı?
           • Evet (да): Eğer a > 0 ise, parabol yukarı doğru bakar ve x-eksenini kesmez (tamamen x-ekseninin üzerinde kalır). Bu durumda ax^2 + bx + c ifadesi her x için pozitiftir. Çözüm kümesi: (-\infty, +\infty) (“всяко х е решение” - her x çözümdür).
           • Hayır (не): Eğer a < 0 ise, parabol aşağı doğru bakar ve x-eksenini kesmez (tamamen x-ekseninin altında kalır). Bu durumda ax^2 + bx + c ifadesi her x için negatiftir. Dolayısıyla ax^2 + bx + c > 0 eşitsizliğinin çözümü yoktur (“няма решение” - çözüm yok).
       • Hayır (не): Eğer b^2 - 4ac \ge 0 ise (Diskriminant \Delta \ge 0 ise):
         • Yedinci Karar Kutusu: b^2 - 4ac = 0 mı? (Diskriminant \Delta = 0 mı?)
           • Evet (да): Eğer diskriminant sıfırsa (çakışık iki kök var):
             • Sekizinci Karar Kutusu: a > 0 mı?
               • Evet (да): Eğer a > 0 ise, parabol yukarı doğru bakar ve x-eksenine teğettir. Teğet noktası x = -b/(2a)'dır. Bu noktada ax^2 + bx + c = 0 olur. Diğer tüm x değerleri için ax^2 + bx + c > 0 olur. Çözüm kümesi: x \neq -b/(2a) (“всяко x \neq -b/(2a) е решение” - x \neq -b/(2a) olan her x çözümdür).
               • Hayır (не): Eğer a < 0 ise, parabol aşağı doğru bakar ve x-eksenine teğettir. Bu durumda ax^2 + bx + c \le 0 olur. Dolayısıyla ax^2 + bx + c > 0 eşitsizliğinin çözümü yoktur (“няма решение” - çözüm yok).
           • Hayır (не): Eğer b^2 - 4ac > 0 ise (Diskriminant \Delta > 0 ise, yani iki farklı reel kök var):
             Kökler: x_1 = (-b - \sqrt{b^2-4ac}) / (2a) ve x_2 = (-b + \sqrt{b^2-4ac}) / (2a).
             • Dokuzuncu Karar Kutusu: a > 0 mı?
               • Evet (да): Eğer a > 0 ise, parabol yukarı doğru bakar. Eşitsizliğin (ax^2+bx+c>0) çözümü köklerin dışındaki bölgelerdir. Çözüm kümesi: (-\infty, (-b - \sqrt{b^2-4ac}) / (2a)) \cup ((-b + \sqrt{b^2-4ac}) / (2a), +\infty).
               • Hayır (не): Eğer a < 0 ise, parabol aşağı doğru bakar. Eşitsizliğin (ax^2+bx+c>0) çözümü köklerin arasındaki bölgedir. (Not: Şemada bu durum için doğrudan bir çözüm aralığı verilmemiş, “няма решения” - çözüm yok bloğuna bağlanmış. Bu, eğer a<0 ve \Delta>0 ise ax^2+bx+c>0 eşitsizliğinin çözümünün kökler arası olması gerektiği gerçeğiyle çelişir. Örneğin, -x^2+3x-2 > 0 eşitsizliğinin kökleri 1 ve 2’dir ve çözüm (1,2)'dir. Şemada bu durum için “çözüm yok” denmesi hatalıdır. Bu akış şemasında a<0 ve \Delta>0 durumu için bir hata bulunmaktadır. Doğru sonuç, kökler arasındaki aralık olmalıdır: ((-b - \sqrt{b^2-4ac}) / (2a), (-b + \sqrt{b^2-4ac}) / (2a)) (köklerin sıralamasına dikkat ederek). Ancak a<0 olduğunda, köklerin formülündeki 2a negatif olacağından, (-b - \sqrt{\Delta})/(2a) daha büyük kök, (-b + \sqrt{\Delta})/(2a) daha küçük kök olur. Bu durumda aralık ( (-b + \sqrt{b^2-4ac}) / (2a), (-b - \sqrt{b^2-4ac}) / (2a) ) şeklinde yazılmalıdır.)

Özetle, şema ax^2 + bx + c > 0 eşitsizliğini çözmek için bir mantıksal süreç sunmaktadır:

1. Önce a'nın sıfır olup olmadığı kontrol edilir. Eğer sıfırsa doğrusal eşitsizlik çözülür.
2. Eğer a sıfır değilse, diskriminant (b^2 - 4ac) incelenir.
   • Diskriminant negatifse, a'nın işaretine göre ya her x çözümdür ya da çözüm yoktur.
   • Diskriminant sıfırsa, a'nın işaretine göre ya teğet noktası hariç her x çözümdür ya da çözüm yoktur.
   • Diskriminant pozitifse, a'nın işaretine göre köklerin dışındaki veya (şemadaki hataya rağmen doğrusu) içindeki aralık çözüm olur.

Şemanın sağ alt köşesindeki “няма решения” (çözüm yok) kutusu, birkaç farklı durumda ulaşılan ortak bir sonuçtur.

Şekil 34 olarak belirtilmiş.