..... matrisin satırca indirgenmiş formunu bulunuz

Eğitim ve Öğretim Matematik
1

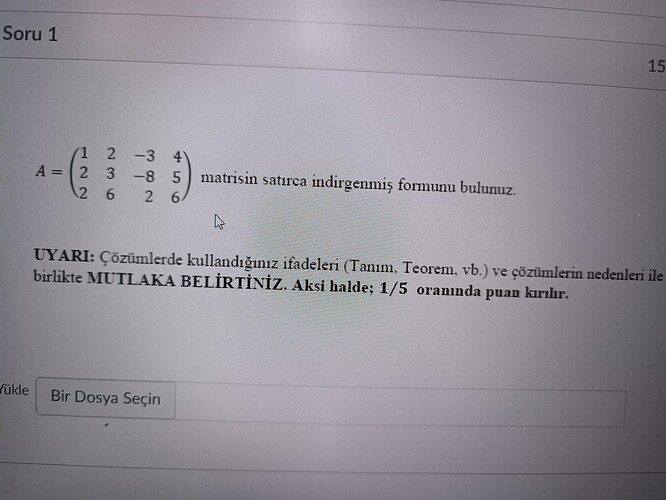
17192994439557591230285612063675
171929944395575912302856120636751920×1440 362 KB

Soru 1

A = \begin{pmatrix} 1 & 2 & -3 & 4 \\ 2 & 3 & -8 & 5 \\ 2 & 6 & 2 & 6 \end{pmatrix} matrisin satırca indirgenmiş formunu bulunuz.

UYARI: Çözümlerde kullandığınız ifadeleri (Tanım, Teorem, vb.) ve çözümlerin nedenleri ile birlikte MUTLAKA BELİRTİNİZ. Aksi halde: 1/5 oranında puan kırılır.

Bu resim, satır indirgeme işlemleri üzerine bir matematik sorusunu içermektedir. Soruda verilen matrisin satırca indirgenmiş formunun bulunması istenmektedir. Ayrıca çözümde kullanılan ifadelerin ve nedenlerin belirtilmesi gerektiği vurgulanmaktadır.

2

Satır Eşelonu ve Satır İndirgenmiş Matris

Bir matrisin satır indirgenmiş formunu (row-reduced echelon form, RREF) bulmak, matrisin sıfır olmayan pivot elemanlarının hepsinin 1 olduğu ve bu elemanların üzerinde ve altında sıfırların bulunduğu bir forma getirilmesi anlamına gelir. Bu işlem, Gauss-Jordan eleme yöntemi ile yapılır.

Aşama 1: İndirgeyici Satır Operasyonları

Matrisin her satırını, diğer satırları etkilemeyecek şekilde sıfır olmayan bir değere sahip olacak şekilde işlemler uygulayarak, pivot elemanlarını yaratırız. Bu işlemleri adım adım yapalım.

Adım 1: İlk pivot elemanı oluşturma (1. Satır, 1. Sütun)

A = \begin{pmatrix} 1 & 2 & -3 & 4 \\ 2 & 3 & -8 & 5 \\ 2 & 6 & 2 & 6 \end{pmatrix}

İlk satır zaten 1 ile başlıyor, bu yüzden pivot eleman 1’dir. İkinci ve üçüncü satırları bu pivot elemanı kullanarak sıfırlayalım.

2. satır = 2. satır - 2 * 1. satır
3. satır = 3. satır - 2 * 1. satır

Yeni matris:
A = \begin{pmatrix} 1 & 2 & -3 & 4 \\ 0 & -1 & -2 & -3 \\ 0 & 2 & 8 & -2 \end{pmatrix}

Adım 2: İkinci pivot elemanı oluşturma (2. Satır, 2. Sütun)

  1. satır, 2. sütundaki pivot eleman -1’dir. Bunu 1 yapalım:
2. satır = -1 * 2. satır

A = \begin{pmatrix} 1 & 2 & -3 & 4 \\ 0 & 1 & 2 & 3 \\ 0 & 2 & 8 & -2 \end{pmatrix}

Şimdi ikinci pivot elemanı kullanarak 1. ve 3. satırdaki 2. sütunu sıfırlayalım:

1. satır = 1. satır - 2 * 2. satır
3. satır = 3. satır - 2 * 2. satır

Yeni matris:
A = \begin{pmatrix} 1 & 0 & -7 & -2 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 4 & -8 \end{pmatrix}

Adım 3: Üçüncü pivot elemanı oluşturma (3. Satır, 3. Sütun)

  1. satır, 3. sütundaki pivot eleman 4’tür. Bunu 1 yapalım:
3. satır = 1/4 * 3. satır

A = \begin{pmatrix} 1 & 0 & -7 & -2 \\ 0 & 1 & 2 & 3 \\ 0 & 0 & 1 & -2 \end{pmatrix}

Şimdi üçüncü pivot elemanını kullanarak 1. ve 2. satırdaki 3. sütunu sıfırlayalım:

1. satır = 1. satır + 7 * 3. satır
2. satır = 2. satır - 2 * 3. satır

Sonuç olarak satırca indirgenmiş matris:
A = \begin{pmatrix} 1 & 0 & 0 & 12 \\ 0 & 1 & 0 & 7 \\ 0 & 0 & 1 & -2 \end{pmatrix}

Sonuç

Bu matrisin satır indirgenmiş formuna ulaşmak için uyguladığımız satır eşelonu işlemleri sonucu elde ettiğimiz matris:
A = \begin{pmatrix} 1 & 0 & 0 & 12 \\ 0 & 1 & 0 & 7 \\ 0 & 0 & 1 & -2 \end{pmatrix}

TERİMLER:

Satır İndirgenmiş Matris (RREF): Bir matrisin tüm sıfır olmayan satırlarının pivot elemanları 1 olan ve bu pivot elemanların üzerinde ve altında sıfırlar bulunan hali.