Height
60°
10 m
Kısa Cevap:
Direğin yüksekliği 10 \cdot \tan(60^\circ) = 10 \cdot \sqrt{3} \approx 17.32 metredir.
Detaylı Açıklama
Çözüm
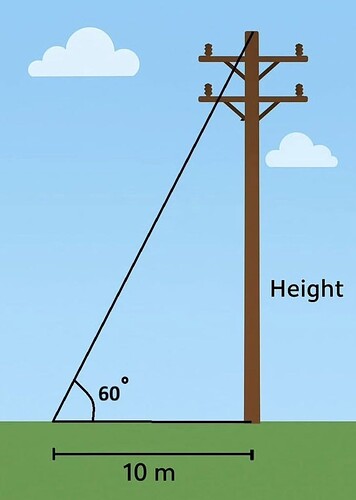
- Sorudaki şekil bir dik üçgen oluşturuyor:
- Yükseklik: Direğin boyu (h)
- Taban: 10 metre
- Hipotenüs: Tel
- Açı (taban ile tel arasındaki açı): 60^\circ
Dik üçgende tanjant fonksiyonu:
\tan(\theta) = \frac{\text{karşı kenar}}{\text{komşu kenar}}
Burada,
- \theta = 60^\circ
- Karşı kenar = height (direk yüksekliği, h)
- Komşu kenar = taban (10\,m)
Formülü yerine koyarsak:
\tan(60^\circ) = \frac{h}{10}
\tan(60^\circ) = \sqrt{3}\approx 1.732
Bunu yerine yazalım:
1.732 = \frac{h}{10} \implies h = 10 \cdot 1.732 = 17.32\,\text{metre}
Kısa Özet
- \boxed{h = 17.32\,\text{metre}}
TERİMLER:
- \tan(\theta) (Tanjant): Bir dik üçgende belirli bir açının karşı kenarının, komşu kenara oranıdır.
- Hipotenüs: Dik üçgende dik açıya komşu olmayan en uzun kenar.
Daha fazla açıklama istersen, detaylandırabilirim!
1 Beğeni