Parkın köşeleri ile A, B, C ve D noktalarına aydınlatma direği dikileceğine göre yeşil alanların etrafında en az kaç aydınlatma direği bulunur?

, ,
1

CEVAP NE

8
81391×913 19.5 KB

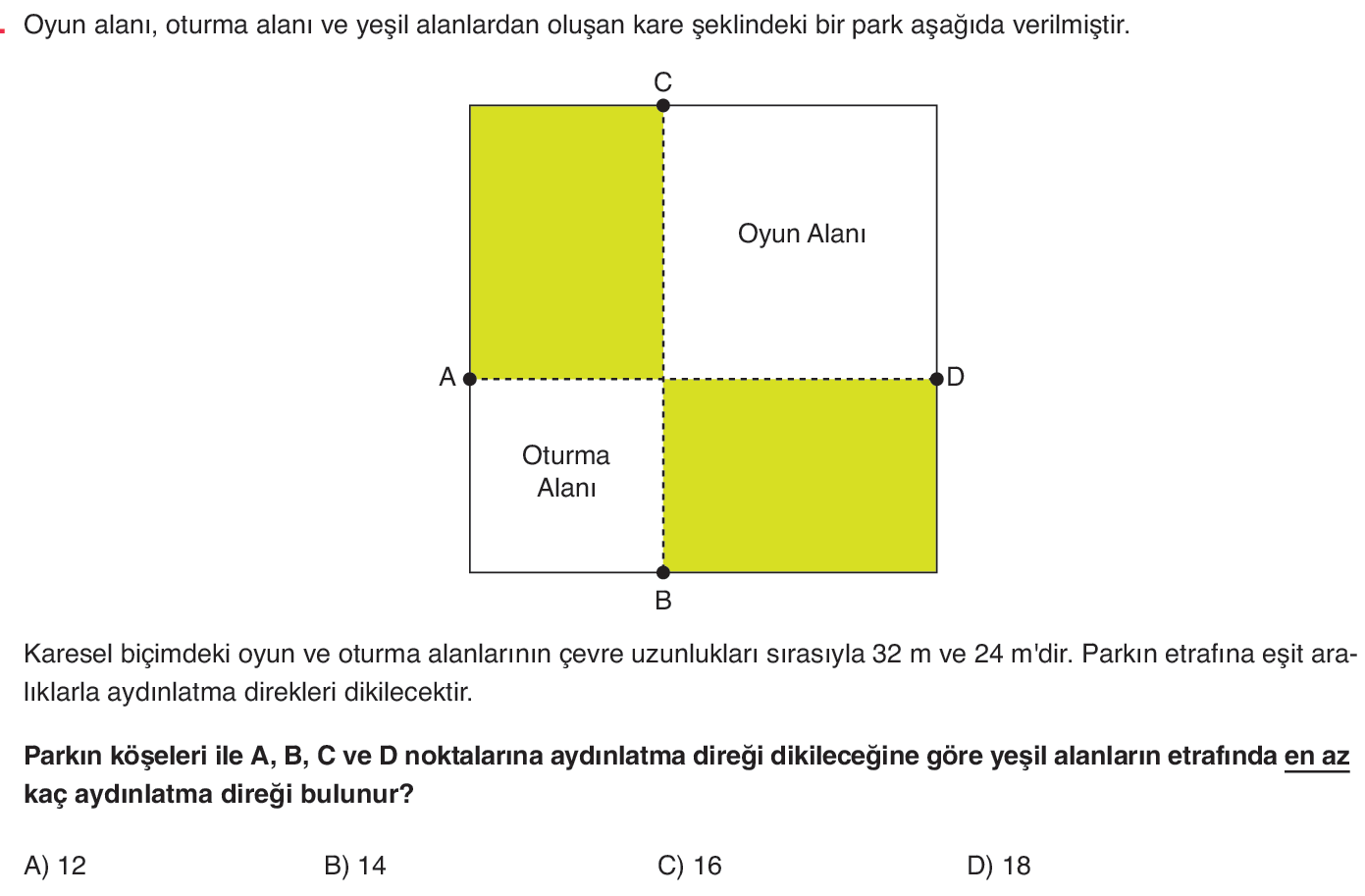
  • Oyun alanı, oturma alanı ve yeşil alanlardan oluşan kare şeklindeki bir park aşağıda verilmiştir.

Oyun Alanı
Oturma Alanı
A
B
C
D

Karesel biçimdeki oyun ve oturma alanlarının çevre uzunlukları sırasıyla 32 m ve 24 m’dir. Parkın etrafına eşit aralıklarla aydınlatma direkleri dikilecektir.

Parkın köşeleri ile A, B, C ve D noktalarına aydınlatma direği dikileceğine göre yeşil alanların etrafında en az kaç aydınlatma direği bulunur?

A) 12
B) 14
C) 16
D) 18

2

Doğru cevap: B) 14

Çözümün kısa açıklaması

  • Büyük karenin bir kenarını s kabul edelim. Oyun alanının çevresi 32\, m, oturma alanının çevresi 24\, m verildiğine göre s=14\, m ve bölücüler arasındaki uzaklıkların toplamı x+y=12\, çıkar.
  • Park çevresine eşit aralıklarla direk dikilecek; köşeler ile A,B,C,D noktalarının da direk olduğu biliniyor. Bu şartla en büyük aralık 2\, m olur (uygun x seçilirse), böylece park çevresine yerleştirilecek direklerin yarısı yeşil alanların etrafında kalır ve sayı 28/2=14 olur.

Detaylı adımlar

  1. Büyük karenin kenarı s.

    • Üst sağ (oyun) alanı bir dikdörtgen/intern küçük alan; çevresi 32\Rightarrow 2[(s-x)+(s-y)]=32 ⇒ 2s-x-y=16.
    • Alt sol (oturma) alanı çevresi 24\Rightarrow 2(x+y)=24 ⇒ x+y=12.
    • Birinci denklemden 2s-(x+y)=16 yerine koyunca 2s-12=16 ⇒ 2s=28 ⇒ s=14.

  2. Park çevresi 4s=56\, m. Dıştaki özel noktalar (köşeler, A,B,C,D) çevre üzerinde aralıklı; bu noktalar arasındaki parçaların uzunlukları x,\;14-x,\;x+2,\;12-x gibi ifadelerle verilir. Eşit aralıkla direk dikilmesi için bu parça uzunluklarının ortak böleni (en büyük ortak uzunluk) gereklidir.

    • Genel olarak bu ortak bölen g=\gcd(x,14-x,x+2,12-x) olur. Matematiksel sadeleştirme ile g=\gcd(x,2,14) bulunur.
    • Buna göre x çiftse g=2, x tekse g=1. En az direk sayısını elde etmek için (en büyük aralığı almak için) x çift seçilebilir ve g=2 alınır.

  3. Eğer aralık g=2\, m ise toplam direk sayısı N=56/2=28. Yeşil alanların dış kenarları park çevresinin toplam 28\, m’lik yarısını kapladığından yeşil alanların etrafındaki direk sayısı 28/2=14 olur.

Sonuç: En az 14 aydınlatma direği bulunur.

TERİMLER:

gcd (EBOB): İki veya daha fazla tamsayının en büyük ortak böleni; burada uzunlukların ortak böleni olarak eşit aralığın en büyük mümkün değeri.