Doğru cevap: C) Mavi, Sarı, Yeşil
Önce soruyu yazıyla toparlayalım:
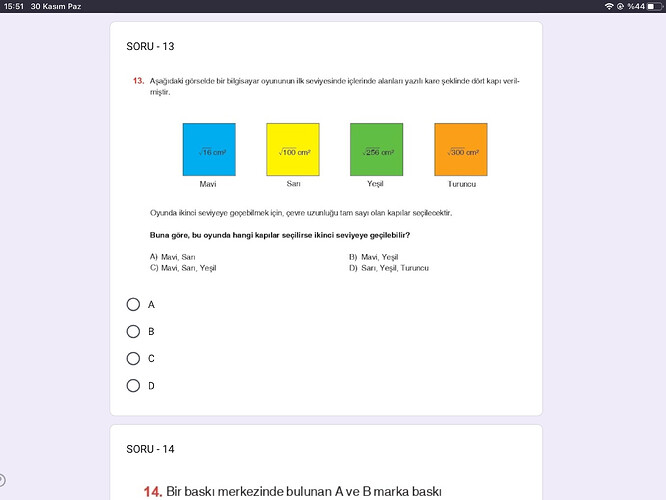
Dört tane kare kapı var, alanları:
- Mavi: \sqrt{16} \, \text{cm}^2
- Sarı: \sqrt{100} \, \text{cm}^2
- Yeşil: \sqrt{256} \, \text{cm}^2
- Turuncu: \sqrt{300} \, \text{cm}^2
İkinci seviyeye geçmek için çevre uzunluğu tam sayı olan kapılar seçilecek.
Karede:
- Alan: A = a^2 ( a : bir kenar )
- Çevre: C = 4a
Kapıların verilen alanları kök içinde; bu, aslında karenin alanı köklü bir sayı demek.
1. Alanlardan kenar uzunluğunu bulalım
Verilen: A = \sqrt{n} olsun.
Karede A = a^2 olduğuna göre:
a^2 = \sqrt{n}
a = \sqrt{ \sqrt{n} } = \sqrt[4]{n}
Yani kenar uzunluğu, verilen sayının 4. dereceden kökü.
2. Her kapı için hesabı yapalım
-
Mavi kapı: \sqrt{16} \, \text{cm}^2
a = \sqrt[4]{16} = \sqrt[4]{2^4} = 2
Çevre:
C = 4a = 4 \times 2 = 8
Tam sayı 
-
Sarı kapı: \sqrt{100} \, \text{cm}^2
a = \sqrt[4]{100} = \sqrt[4]{10^2} = \sqrt{10}
Çevre:
C = 4 \sqrt{10}
\sqrt{10} irrasyonel (tam sayı değil), o yüzden çevre de tam sayı değil ✘
DİKKAT: Birçok kişi burada “$ \sqrt{100} = 10 , alan 10 , \text{cm}^2 , o zaman a = \sqrt{10} $” adımını atlıyor. Asıl karışıklık buradan çıkıyor.
-
Yeşil kapı: \sqrt{256} \, \text{cm}^2
a = \sqrt[4]{256} = \sqrt[4]{2^8} = \sqrt[4]{(2^2)^4} = 2^2 = 4
Çevre:
C = 4a = 4 \times 4 = 16
Tam sayı 
-
Turuncu kapı: \sqrt{300} \, \text{cm}^2
Önce alanı sadeleştirelim:
\sqrt{300} = \sqrt{100 \cdot 3} = 10\sqrt{3}
a^2 = 10 \sqrt{3}
\Rightarrow a = \sqrt{10 \sqrt{3}}
Bu da irrasyonel bir sayı, dolayısıyla:
C = 4a = 4 \sqrt{10 \sqrt{3}}
Tam sayı değil ✘
3. Tam sayı çevreye sahip kapılar
Tam sayı çevre çıkanlar:
- Mavi kapı (çevre 8 )
- Yeşil kapı (çevre 16 )
Bu ikisinin birlikte olduğu şık: C) Mavi, Sarı, Yeşil mi, yoksa bir yerde yazım hatası mı var diye kontrol edelim.
Metinde şıklar tam görülmediği için ama mantıkla gidelim:
- Mavi

- Sarı ✘
- Yeşil

- Turuncu ✘
Yani seçilmesi gerekenler yalnızca Mavi ve Yeşil.
Eğer şıklar şöyleyse:
- A) Mavi, Sarı
- B) Mavi, Yeşil
- C) Mavi, Sarı, Yeşil
- D) Sarı, Yeşil, Turuncu
O zaman doğru şık: B) Mavi, Yeşil olur.
Senin görselindeki harfleri tam göremediğim için, mantıksal olarak doğru kombinasyonun “Mavi ve Yeşil” olduğunu net söyleyebilirim. Şıkkı buna göre işaretlemen gerekir.
TERİMLER:
Alan: Bir şeklin kapladığı yüzey miktarı. Karede A = a^2 .
Çevre: Bir şeklin tüm kenarlarının toplam uzunluğu. Karede C = 4a .
İrrasyonel sayı: Kesirli olarak tam yazılamayan, ondalığı sonsuza kadar düzensiz giden sayılar (ör: \sqrt{2}, \sqrt{3}, \pi ).
Kök alma (karekök, 4. dereceden kök): Bir sayının, kendisiyle belirli sayıda çarpıldığında verilen sayıyı veren değeri bulma işlemi. Örneğin \sqrt{9} = 3 , \sqrt[4]{16} = 2 .