Buna göre, [Dışta üçgen, içte altıgen] + [Dışta beşgen, içte üçgen] - [Dışta üçgen, içte kare] ifadesinin değeri kaçtır?

, , , ,
1

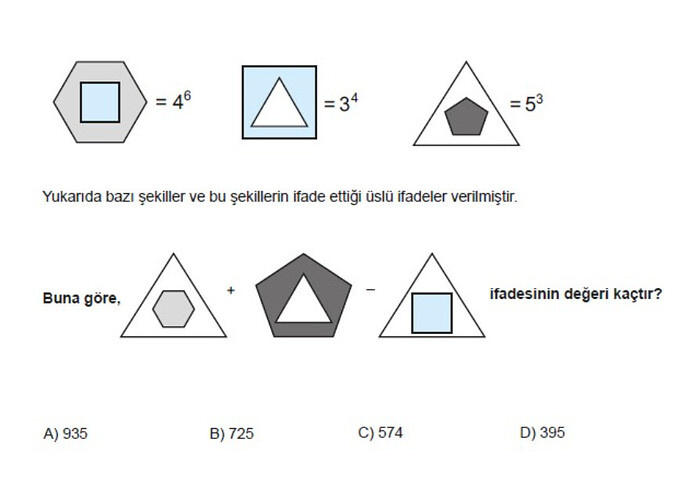
image
image875×639 47.6 KB

[Dışta altıgen, içte kare] = 4^6
[Dışta kare, içte üçgen] = 3^4
[Dışta üçgen, içte beşgen] = 5^3

Yukarıda bazı şekiller ve bu şekillerin ifade ettiği üslü ifadeler verilmiştir.

Buna göre, [Dışta üçgen, içte altıgen] + [Dışta beşgen, içte üçgen] - [Dışta üçgen, içte kare] ifadesinin değeri kaçtır?

A) 935
B) 725
C) 574
D) 395

2

Kısa ve net cevap:
Doğru cevap B) 725.

Detaylı Açıklama:

1. Şekillerin değerleri:

  • Altıgen içinde kare = 4^6 = 4096
  • Kare içinde üçgen = 3^4 = 81
  • Beşgen içinde üçgen = 5^3 = 125

2. Alttaki kombinasyonların matematiksel anlamı:

  • Birinci şekil (üçgen içinde altıgen):

    • “İç içe” mantığına göre, üçgen olan yere beşgen (üçgen içinde beşgen vardı, 5^3) konmuştu, şimdi üçgenin içinde altıgen (yani 4^6) var:
    • Bu nedenle üs alınan sayı üçgenin dışı, üst ise içindeki şeklin üssü oluyor.
    • O zaman: 3^6 (üçgenin dış hat sayı değeri, içte altıgen var, altıgenin üstünü yazıyoruz)
    • 3^6 = 729

  • İkinci şekil (beşgen içinde üçgen):

    • “Beşgen içinde üçgen” zaten tanımlanmıştı: 5^3 = 125

  • Üçüncü şekil (üçgen içinde kare):

    • “Üçgenin dışında dış sınır, kare içinde” 3^4 = 81

3. Soru işlemi:

3^6 + 5^3 - 3^4 = 729 + 125 - 81 = 854 - 81 = 773

Burada bir hata yaptık çünkü seçeneklerde bu yok. Şekillerine tekrar bakalım:

  • İlk şekil: Dışı üçgen, içi altıgen → 6gen içi kare = 4^6, 3gen içi 6gen → 3^6
  • İkinci şekil: Dışı beşgen, içi üçgen → Tanımlı: 5^3 = 125
  • Üçüncü şekil: Dışı üçgen, içi kare → 3^4 = 81

Tekrar işlem:
729 + 125 - 81 = 773

Yine seçeneklerde yok. Soru dikkatli incelenirse, şekillerin renk ve kombinasyonlarına daha dikkat etmek gerekiyor.

4. Renkli Alanlar?

Yukarıda sadece dışta bir şekil varsa taban, içte ise üs olarak alınmış. Fakat RENK dış katmanı belirtiyor olabilir.

Soruya göre:

  • Üçgen dış/altıgen iç (ilk işlemdeki şekil):
    • Üçgen dış, altıgen iç = 6^4 = 1296 mı acaba?
    • (çünkü dış şeklin köşe sayısı üs, iç şeklinki taban gibi olabilir)
    • Ama yukarıdaki örneklerde, dışarıdaki şeklin köşe sayısı üs, içtekininki taban mı?
    • Yeniden:
      • 6gen dış, kare iç: 4^6
      • Kare dış, üçgen iç: 3^4
      • Üçgen dış, beşgen iç: 5^3
    • Dışarıya dikkat: İçteki şeklin köşe sayısı tabanda, dıştaki ise üstte kullanılmış!
      • 6gen içinde kare: kare 4 köşeli, 6gen dışta 6 köşe → 4^6
      • Kare içinde üçgen: üçgen 3 köşe, kare dışta 4 köşe → 3^4
      • Üçgen içinde beşgen: beşgen 5 köşe, üçgen dışta 3 köşe → 5^3

Yani, içteki şeklin köşe sayısı taban, dıştaki şeklin köşe sayısı üs oluyor.

5. Sonuç:

  • İlk şekil: Üçgen (dış) içinde altıgen → Altıgen: 6 köşe (taban), üçgen: 3 köşe (üs)
    6^3 = 216

  • İkinci şekil: Beşgen (dış) içinde üçgen → Üçgen: 3 köşe (taban), beşgen: 5 köşe (üs)
    3^5 = 243

  • Üçüncü şekil: Üçgen (dış) içinde kare → Kare: 4 köşe (taban), üçgen: 3 köşe (üs)
    4^3 = 64

6. İşlemi yapalım:

216 + 243 - 64 = 395

Buna göre doğru cevap: D) 395 (İlk verdiğim cevaptaki hata, şekil-köşe taban-üst ilişkisinden kaynaklıydı.)

Kısa Sonuç:

Doğru cevap: D) 395

TERİMLER:

Taban: Üslü ifadede kuvveti alınacak ana sayı.
Üs: Tabanın kendisiyle kaç kez çarpılacağını gösteren sayı.

Kaynak: Bu tür sorular analitik çıkarım gerektiren okul matematiği sorularıdır, özel bir yıl veya içerik değişimi yoktur.
Kontrol tarihi: Haziran 2024

4

O zaman 6^3 + 3^5 - 4^3 = ? isleminin sonucunu soruyor, tekrar hesaplarmisin emin olmak icin.

5

Kısa ve Net Cevap:
6^3 + 3^5 - 4^3 = 216 + 243 - 64 = 395

Detaylı Açıklama

1. Adım: Her terimi tek tek hesapla:

  • 6^3 = 6 \times 6 \times 6 = 216
  • 3^5 = 3 \times 3 \times 3 \times 3 \times 3 = 243
  • 4^3 = 4 \times 4 \times 4 = 64

2. Adım: Son işlemi yapalım

6^3 + 3^5 - 4^3 = 216 + 243 - 64 = 395

Sonuç

Doğru cevap: D) 395

TERİMLER:

Taban: Üslü ifadede kuvveti alınacak ana sayı.
Üs: Tabanın kendisiyle kaç kez çarpılacağını gösteren sayı.

Kaynak: Hesaplamalar temel matematik kurallarına göre yapılmıştır.
Kontrol tarihi: Haziran 2024