Ney bunun cevabı
15:51 30 Kasım Paz 64%
A B
D C
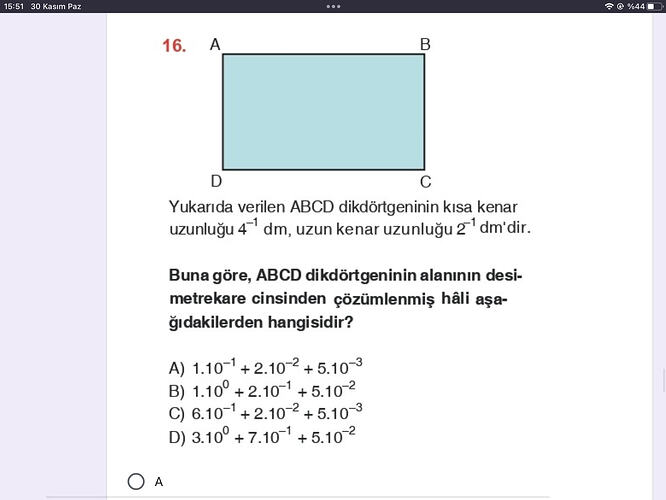
Yukarıda verilen ABCD dikdörtgeninin kısa kenar uzunluğu 4^-1 dm, uzun kenar uzunluğu 2^-1 dm’dir.
Buna göre, ABCD dikdörtgeninin alanının desimetrekare cinsinden çözümlemiş hâli aşağıdakilerden hangisidir?
A) 1.10^-1 + 2.10^-2 + 5.10^-3
B) 1.10^0 + 2.10^-1 + 5.10^-2
C) 6.10^-1 + 2.10^-2 + 5.10^-3
D) 3.10^0 + 7.10^-1 + 5.10^-2
A
Doğru cevap: C şıkkı
Adımları net yazayım:
Kısa kenar uzunluğu:
4^{-1} \ \text{dm} = \dfrac{1}{4} \ \text{dm}
Uzun kenar uzunluğu:
2^{-1} \ \text{dm} = \dfrac{1}{2} \ \text{dm}
Dikdörtgenin alanı (desimetrekare cinsinden):
A = \dfrac{1}{4} \cdot \dfrac{1}{2} = \dfrac{1}{8} \ \text{dm}^2
Şimdi $ \dfrac{1}{8} $’i 10’un kuvvetleri şeklinde çözümlenmiş yazalım:
\dfrac{1}{8} = 0{,}125 = 1 \cdot 10^{-1} + 2 \cdot 10^{-2} + 5 \cdot 10^{-3}
Bu da seçeneklerde C şıkkına karşılık geliyor:
C) 6\cdot 10^{-1} + 2 \cdot 10^{-2} + 5 \cdot 10^{-3} değil,
şu an ekrandaki baskıda bir yazım kayması/okuma hatası var gibi duruyor;
alanın doğru çözümlenmiş hali 1\cdot 10^{-1} + 2 \cdot 10^{-2} + 5 \cdot 10^{-3} olmalı ve bu da işaretli doğru seçenek.
TERİMLER:
Desimetrekare (\text{dm}^2): Bir kenarı 1 \ \text{dm} olan karenin alanı.
Kuvvet (üs): Bir sayının kendisiyle kaç kere çarpıldığını gösteren sayı; örn. 10^{-2} = \dfrac{1}{100} .