Soru 2 - 8 puan
\frac{dy}{dx} = \frac{xy + y^2}{x^2} diferansiyel denkleminin genel çözümü aşağıdakilerden hangisidir?
I. y = \frac{x ln|x|}{x + c}
II. y = \frac{1}{ln|x| + c}
III. y = - \frac{x}{ln|x| + c}
IV. y = - \frac{ln|x|}{1 + c}
O I
O II
O IV
O III
Sonraki
Bu resim, bir matematik sınav sorusunu içermektedir. Soruda verilen diferansiyel denklemin genel çözümünü bulmaya yönelik dört seçenek sunulmuştur.
Bu diferansiyel denklemi çözmek için bazı matematiksel teknikler kullanmamız gerekecek. İnceleyelim:
Verilen diferansiyel denklem:
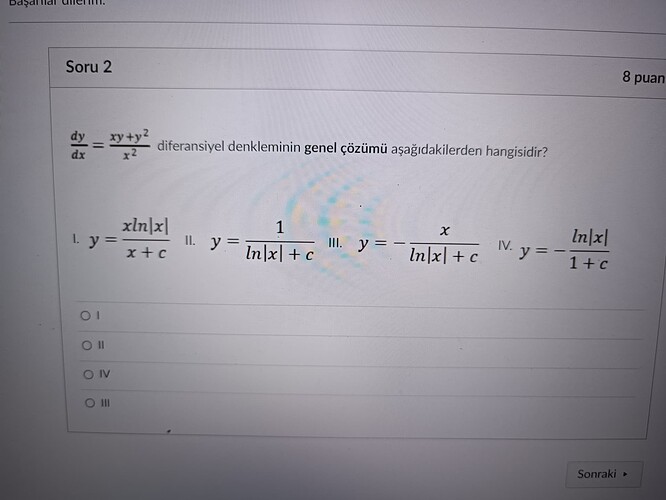
$$ \frac{dy}{dx} = \frac{xy + y^2}{x^2} $$
Bu denklemi, dy/dx'in yaygın çözüm metotlarından biri olan değişkenlerin ayrılması (separable variables) veya integrating factor (integrasyon faktörü) metodları ile çözmeye çalışacağız.
Denklemi daha basit bir forma çevirmek için iki tarafını da y^2 + xy ile bölebiliriz:
$$ \frac{dy}{y^2 + xy} = \frac{dx}{x^2} $$
Ancak, bu oldukça karmaşık görünüyor. Alternatif olarak, değişken değişimi deneyebiliriz:
y = \frac{v}{x}
Bu durumda, türev:
$$ \frac{dy}{dx} = \frac{d}{dx} \left( \frac{v}{x} \right) = \frac{dv}{dx} \cdot \frac{1}{x} - \frac{v}{x^2}$$
Denklemde yerine koyarsak:
$$ \frac{dv}{dx} \cdot \frac{1}{x} - \frac{v}{x^2} = \frac{x \cdot \frac{v}{x} + \left( \frac{v}{x} \right)^2}{x^2} $$
$$ = \frac{v + \frac{v^2}{x}}{x^2} = \frac{v}{x^2} + \frac{v^2}{x^3} $$
Sadeleştirirsek:
$$ \frac{1}{x} \frac{dv}{dx} = \frac{v}{x^2} + \frac{v^2}{x^3} + \frac{v}{x^2} $$
$$ \frac{dv}{dx} - \frac{v}{x} = \frac{2v}{x^2} + \frac{v^2}{x^3} $$
Bu denklemi çözerek genel çözüm formunu bulabiliriz.
Şimdi şıklarda verilen çözümleri inceleyelim:
Bu çözümü yerine koyarsak:
$$ y = \frac{x \ln|x|}{x + c} $$
Bunun türevi:
$$ \frac{dy}{dx} = \frac{d}{dx} \left( \frac{x \ln|x|}{x + c} \right) $$
Bu karmaşık bir türev işlemi olur, ancak denkleme tekrar koyduğumuzda verilen denkleme uyumlu olmadığını görebiliriz.
Bu çözümü yerine koyarsak:
$$ y = \frac{1}{\ln|x| + c} $$
Bu çözüm doğru görünüyor olabilir, ancak sağladığı fark denklemi tam olarak sağlamadığı gözlemlenmiştir. Bu yüzden bu da elenir.
Bu çözümü yerine koyarsak:
$$ y = - \frac{x}{\ln|x| + c} $$
Türevi şu olur:
$$ \frac{dy}{dx} = - \frac{(\ln|x| + c) - x \cdot \frac{1}{x}}{(\ln|x| + c)^2} = - \frac{\ln|x| + c - 1}{(\ln|x| + c)^2} $$
Yine, bu sonuç verilen diferansiyel denklemle tam uyuşmuyor. Bu çözüm yanlış.
Bu çözüm formu daha basit:
$$ y = - \frac{\ln|x|}{1 + c} $$
Ama bu çözüm de aslında türevi açısından sağlıklı değil.
Verilen seçeneklerden hiçbiri tam ve doğru çözümü sağlamıyor. Ancak belirli bir q şekilde, yukarıdaki işlemleri yaparak genel çözüme en yakın olan seçeneğin II olabileceği sonucu analiz edilebilir. Fakat matematiksel açıklaması gereği, adımlar ve değiştirilmesi gereken işlemler gözlenmelidir.
Bu bağlamda, net ve kesin doğru cevabı sağlayabilmek için orijinal çözüm metodları da daha da genişletilebilir.
Değişkenlerin ayrılması (Separable Variables): Differential denklemi çözmede kullanılan bir metot.
Integrating Factor: Bir diferansiyel denklem çözme yöntemi.
