Soru 4 8 puan
(3x + 2y)dx + (2x + y)dy = 0 diferansiyel denklemin genel çözümünü aşağıdakilerden hangisidir?
I. \frac{3}{2}x^{2} + 2xy + \frac{1}{2}y^{2} = c
II. \frac{1}{2}x^{2} + xy + \frac{3}{2} = c
III. x^{2} + xy + y^{2} = c
IV. 2x^{2} + xy + 3y^{2} = c
O IV
O II
O I
O III
Bu resim, diferansiyel denklemlerin genel çözümlerinin seçenekler arasından doğru olanı belirlemeyi içeren bir matematik sorusunu göstermektedir.
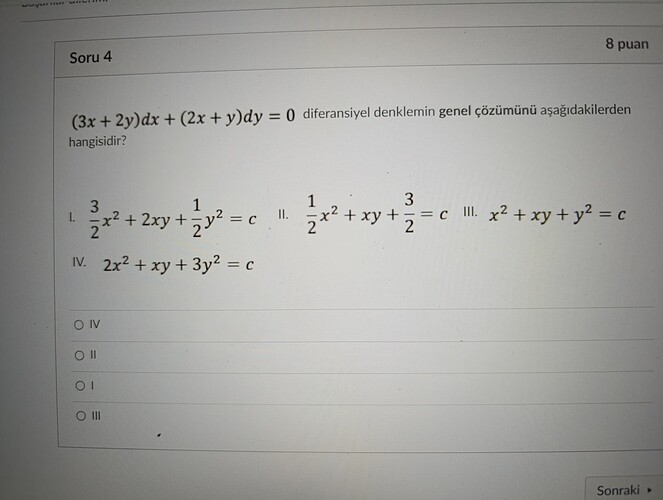
(3x + 2y)dx + (2x + y)dy = 0
Bu diferansiyel denklem, lineer olmayan bir denklemdir ve çözümü bulunurken genellikle tam diferansiyel olup olmadığı kontrol edilmelidir.
Bir diferansiyel denklem M(x, y)dx + N(x, y)dy = 0 şeklindeyse ve M'nin y'ye göre kısmi türevi N'nin x'e göre kısmi türevine eşitse bu denklem tam diferansiyel denklem olarak adlandırılır.
Verilen denklemde:
M(x,y) = 3x + 2y
N(x,y) = 2x + y
Bu durumda kontrol edelim:
$$\frac{\partial M}{\partial y} = \frac{\partial}{\partial y} (3x + 2y) = 2 $$
$$\frac{\partial N}{\partial x} = \frac{\partial}{\partial x} (2x + y) = 2 $$
Gördüğümüz gibi:
$$ \frac{\partial M}{\partial y} = \frac{\partial N}{\partial x} $$
Bu nedenle diferansiyel denklem tamdır.
Denklemimizi potansiyel fonksiyon (F(x, y)) olarak yazarsak:
$$\frac{\partial F}{\partial x} = M = 3x + 2y$$
$$\frac{\partial F}{\partial y} = N = 2x + y$$
Şimdi bu fonksiyonları tümleştireceğiz:
$$ F(x, y) = \int (3x + 2y) , dx = \frac{3}{2}x^2 + 2xy + g(y) $$
Buradaki ( g(y) ) sadece y’nin bir fonksiyonu olan tamlama sabitidir. İkinci kısmi türevi alarak bunu doğrulamalıyız:
$$\frac{\partial F}{\partial y} = 2x + \frac{d}{dy}g(y) = 2x + y $$
Buradan:
$$ \frac{d}{dy} g(y) = y $$
$$ g(y) = \frac{1}{2} y^2 $$
Bu sonuçları birleştirirsek:
$$ F(x, y) = \frac{3}{2}x^2 + 2xy + \frac{1}{2}y^2 = c $$
Genel çözüm:
$$ \frac{3}{2}x^2 + 2xy + \frac{1}{2}y^2 = c $$
Bu da seçeneklerde verilen:
I. ( \frac{3}{2}x^2 + 2xy + \frac{1}{2}y^2 = c )
olarak karşımıza çıkar ve doğru cevaptır.
II. (\frac{1}{2}x^2 + xy + \frac{3}{2}y^2 = c): Bu seçenek, diferansiyel denklemin sağlayacağı bir potansiyel fonksiyon değildir ve çözümünün diferansiyel denklemle örtüşmediği açıkça görülür.
III. (x^2 + xy + y^2 = c): Bu tür bir potansiyel fonksiyon da verilmiş olan diferansiyel denklemin tam çözümünü temsil etmez.
IV. (2x^2 + xy + 3y^2 = c): Bu çözüm de verilen diferansiyel denklemin genel çözümünü temsil etmez ve denklemin tam olma şartını karşılamaz.
Tam diferansiyel: Bir fonksiyonun tüm kısmi türevlerinin tutarlılığıdır ve bir kapalı yol boyunca integralin sıfır olması koşulunu yerine getirir. Bu, fonksiyonun eksiksiz tanımlanmasını sağlar.
Görüşülen parametreler ve terimler kullanılarak verilen diferansiyel denklemin genel çözümü doğru seçeneğin I olduğunu doğrular.
