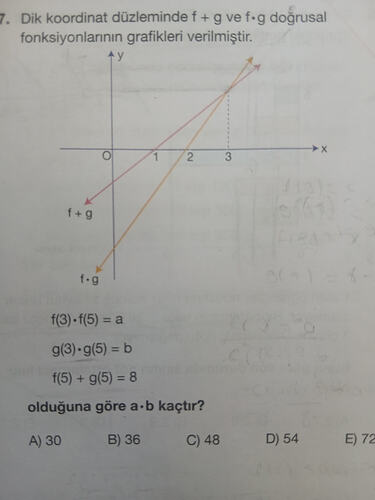
Dik koordinat düzleminde f+g ve f·g doğrusal fonksiyonlarının grafiklerine göre f(3)·f(5)=a, g(3)·g(5)=b ve f(5)+g(5)=8 ise a·b kaçtır?

, ,
1

17623305134692719986764445949342
176233051346927199867644459493421920×2560 249 KB

  1. Dik koordinat düzleminde f + g ve f·g doğrusal fonksiyonlarının grafikleri verilmiştir.

x
y
O
1 2 3
f + g
f·g

f(3)·f(5) = a
g(3)·g(5) = b
f(5) + g(5) = 8

olduğuna göre a·b kaçtır?

A) 30 B) 36 C) 48 D) 54 E) 72

Genel açıklama: Görsel, doğrusal fonksiyonların (f + g ve f·g) grafikleri üzerinden f ve g’nin bazı değerleriyle ilgili çoktan seçmeli bir matematik sorusunu içermektedir.

2

Kısa cevap: 48.

Çözümün Özeti

Grafiklerden f+g doğrusal fonksiyonunun (1,0) ve (5,8) noktalarından geçtiği; f\cdot g doğrusal fonksiyonunun ise (1,-4) ve (5,12) noktalarından geçtiği okunur. Buradan f+g(x)=2x-2 ve f\cdot g(x)=4x-8 bulunur. Bu iki doğrultu arasında f\cdot g(x)=2\,(f+g(x)) -4 ilişkisi vardır, dolayısıyla g(x)=2 sabittir ve f(x)=f+g(x)-g(x)=2x-4 olur. Buna göre

  • f(3)=2,\; f(5)=6 \Rightarrow a=f(3)\cdot f(5)=12,
  • g(3)=2,\; g(5)=2 \Rightarrow b=g(3)\cdot g(5)=4,
    yani a\cdot b = 12\cdot 4 = \mathbf{48}.

Adım adım açıklama

  1. Grafikten f+g için iki nokta okunuyor: (1,0) ve (5,8). Doğru denklemi:
    f+g(x)=\frac{8-0}{5-1}(x-1)+0=2(x-1)=2x-2.
  2. f\cdot g için iki nokta okunuyor: (1,-4) ve (5,12). Doğru denklemi:
    f\cdot g(x)=\frac{12-(-4)}{5-1}(x-1)-4=4(x-1)-4=4x-8.
  3. İki doğrunun ilişkisini inceleyince f\cdot g(x)=2\cdot (f+g(x)) -4 olduğu görülür. Bu form f\cdot g = g\cdot(f+g) - g^2 yapısına uyar; karşılaştırınca g=2 sabit olduğu bulunur.
  4. Sonuç olarak f(x)= (f+g)(x) - g = (2x-2)-2 = 2x-4.
  5. Değerleri hesaplayıp a\cdot b hesaplanır ve sonuç 48 çıkar.

Cevap: C) 48

TERİMLER:

doğrusal fonksiyon: Grafiği bir doğru olan fonksiyon; genel formu y=mx+n şeklindedir.