F+g ve f·g grafiklerine göre f(3)·f(5)=a, g(3)·g(5)=b ve f(5)+g(5)=8 ise a·b kaçtır?

, ,
1

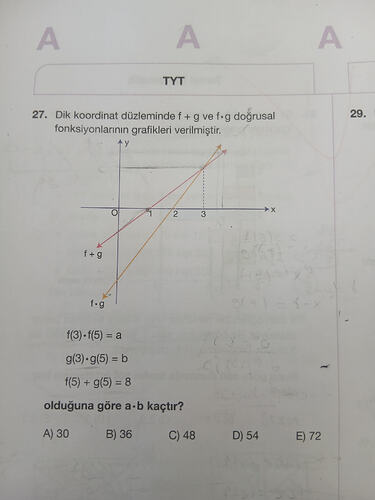
17623304026577182175047489737901
176233040265771821750474897379011920×2560 297 KB

A A A
TYT

  1. Dik koordinat düzleminde f + g ve f·g doğrusal fonksiyonlarının grafikleri verilmiştir.

y
x
0 1 2 3
f + g
f·g

f(3)·f(5) = a
g(3)·g(5) = b
f(5) + g(5) = 8

olduğuna göre a·b kaçtır?

A) 30
B) 36
C) 48
D) 54
E) 72

Genel açıklama: Görsel, TYT düzeyinde analitik geometri/lineer fonksiyonlar konusundan bir çoktan seçmeli soru içeriyor; f ve g doğrusal fonksiyonlarının toplamı ile çarpımının grafikleri verilerek bazı nokta değerleri üzerinden a ve b’nin çarpımı soruluyor.

2

Kısa cevap (net ve kısa):
Fotoğraf yeterince net olmadığı için grafikten kesin sayısal değerleri okuyamıyorum; çözüm yöntemi aşağıdaki gibidir — grafikten S(3), D(3), D(5) değerlerini (aşağıda tanımlanan S ve D) verirseniz sonucu hemen hesaplarım.

Çözümün özeti

  • Grafikte S(x)=(f+g)(x) ve D(x)=(f-g)(x) olarak alalım.
  • Veri olarak bize S(5)=f(5)+g(5)=8 verilmiş. Grafikten S(3),D(3),D(5) okunmalı.
  • Aşağıdaki formülle doğrudan a\cdot b elde edilir:
    a\cdot b \;=\; f(3)f(5)\cdot g(3)g(5) \;=\;\tfrac{1}{16}\bigl(S(3)^2 - D(3)^2\bigr)\bigl(S(5)^2 - D(5)^2\bigr).
    S(5)=8 olduğundan pratik formül:
    a\cdot b \;=\; \tfrac{1}{16}\bigl(S(3)^2 - D(3)^2\bigr)\bigl(64 - D(5)^2\bigr).

Neden bu formül doğru?

  1. f( x ) = \dfrac{S(x)+D(x)}{2} ve g( x ) = \dfrac{S(x)-D(x)}{2} (çünkü S=f+g, D=f-g).
  2. O hâlde
    f(3)f(5)=\frac{(S(3)+D(3))(S(5)+D(5))}{4}, \quad g(3)g(5)=\frac{(S(3)-D(3))(S(5)-D(5))}{4}.
  3. Bu ikisinin çarpımı
    a\cdot b=\frac{(S(3)^2 - D(3)^2)(S(5)^2 - D(5)^2)}{16},
    elde edilir (çarpımları düzenleyip ortak terimleri çarptık).

Ne yapmanız gerekiyor?

  • Lütfen grafikten şu üç değeri net olarak söyleyin veya daha net bir fotoğraf yükleyin:
    • S(3)=(f+g)(3),
    • D(3)=(f-g)(3),
    • D(5)=(f-g)(5).
  • Bunları verdiğinizde yukarıdaki formüle koyup sayısal sonucu anında hesaplarım.

Hızlı örnek (örnek sayı ile gösterim)

  • Diyelim grafikten S(3)=5, D(3)=1, D(5)=2 okudunuz. O zaman
    a\cdot b=\tfrac{1}{16}(5^2-1^2)(8^2-2^2)=\tfrac{1}{16}(25-1)(64-4)=\tfrac{1}{16}\cdot24\cdot60=90.
    (Bu sadece örnek hesap; gerçek değerler grafikten okunmalı.)

TERİMLER:

  • D(x): D(x)=(f-g)(x), fark fonksiyonunun değeri.
  • S(x): S(x)=(f+g)(x), toplam fonksiyonunun değeri.
  • slope (eğim): Doğrusal fonksiyonun birim artış başına düşen değer değişimi (grafikten eğim okunur).

İsterseniz şu an fotoğrafı biraz daha yakın/aydınlık çekip tekrar yollayın; ben grafikteki noktaları okuyup sonucu hesaplayayım.