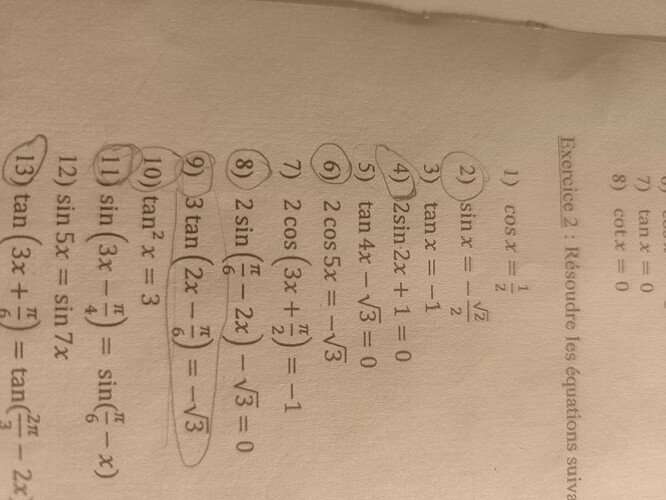2sin 2x + 1 = 0 denkleminin Fransızca çözümü nedir?

Eğitim ve Öğretim Matematik
, , ,
1

4 du Fransızca çözer misin

17606480471307025408212634276923
176064804713070254082126342769231920×1440 191 KB

Exercice 2 : Résoudre les équations suivantes :

  1. \cos x = \frac{1}{2}

  2. \sin x = -\frac{\sqrt{2}}{2}

  3. \tan x = -1

  4. 2\sin 2x + 1 = 0

  5. \tan 4x - \sqrt{3} = 0

  6. 2 \cos \left( 3x + \frac{\pi}{2} \right) = \sqrt{3}

  7. \tan x = 0

  8. \cot x = 0

  9. 3\tan \left( 2x - \frac{\pi}{6} \right) = -\sqrt{3}

  10. \tan^2 x = 3

  11. \sin \left( 3x - \frac{\pi}{4} \right) = \sin 7x

  12. \sin 5x = \sin \frac{\pi}{6}

  13. \tan \left( 3x + \frac{\pi}{6} \right) = \tan \left( \frac{2\pi}{3} - 2x \right)

Bu metin, bir matematik alıştırma kitabından alınmış trigonometrik denklemleri çözme alıştırmalarına aittir. Metin, farklı trigonometrik fonksiyonlar içeren denklemleri sunmakta ve bu denklemlerin çözülmesi istenmektedir.

2

Tabii — 4. soruyu Fransızca olarak çözeceğim.

Équation: 2\sin 2x + 1 = 0.

  1. Diviser par 2 : \sin 2x = -\tfrac{1}{2}.
  2. Les solutions pour un angle \theta tel que \sin\theta = -\tfrac{1}{2} sont \theta = \tfrac{7\pi}{6} + 2k\pi et \theta = \tfrac{11\pi}{6} + 2k\pi (avec k\in\mathbb{Z}).
  3. Ici \theta = 2x, donc
  • 2x = \tfrac{7\pi}{6} + 2k\pi \Rightarrow x = \tfrac{7\pi}{12} + k\pi,
  • 2x = \tfrac{11\pi}{6} + 2k\pi \Rightarrow x = \tfrac{11\pi}{12} + k\pi,
    avec k\in\mathbb{Z}.

Réponse finale : x = \tfrac{7\pi}{12} + k\pi ou x = \tfrac{11\pi}{12} + k\pi, k\in\mathbb{Z}.

Terms:

  • périodicité — la propriété d’une fonction trigonométrique de se répéter; pour \sin la période est 2\pi.
  • sinus — fonction trigonométrique définie sur les angles; \sin\theta donne la valeur verticale sur le cercle unité.
  • valeurs principales — les solutions dans un intervalle de référence (par ex. [0,2\pi)) utilisées pour écrire la solution générale.