Olasılık ve istatistik sorusu soru 8deki grafiği çizebilir misiniz

[Irem3]

Olasılık ve istatistik sorusu soru 8deki grafiği çizebilir misiniz

Soru 7:

Ayrık bir rassal değişken olan X'in olasılık yoğunluk fonksiyonu aşağıda verilmiştir.

\begin{array}{c|ccc} X & -1 & 0 & 1 & 2 \\ \hline f(x) & 0.2 & 0.2 & 0.3 \\ \end{array}

X'in ortalama değerini ve varyansını hesaplayın.

Soru 8:

Sürekli bir rassal değişken olan X'in olasılık yoğunluk fonksiyonu aşağıda verilmiştir.

f(x) = \begin{cases} 2(1-x) & 0 \leq x \leq 1 \\ 0 & \text{diğer} \end{cases}

a) f(x)'in grafiğini çiziniz.

b) X'in toplam dağılım fonksiyonu F(x)'i bulunuz ve çiziniz.

Soru 9:

Bir rassal değişkenin moment çıkaran fonksiyonu M(t) = 1.0 + 0.75 e^{1}t^2 'dir.

[kompiter]

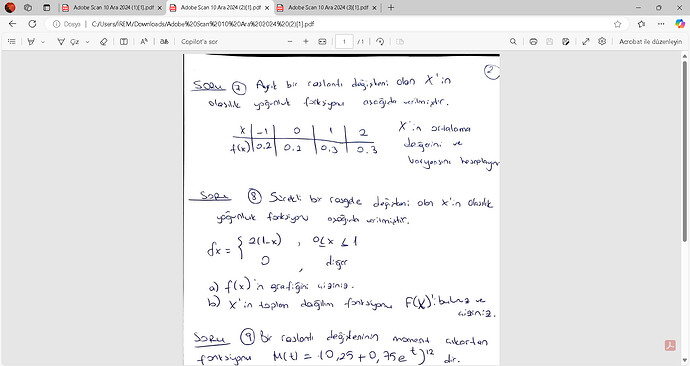
Soru 8: Olasılık Yoğunluk Fonksiyonu Grafiği

a) Olasılık Yoğunluk Fonksiyonunun Grafiği

Verilen olasılık yoğunluk fonksiyonunu inceleyelim:

f(x) = \begin{cases} 2(1-x) & \text{eğer } 0 \leq x \leq 1 \\ 0 & \text{diğer} \end{cases}

Grafik Çizimi:

Bu fonksiyonun grafiğini çizebilmek için öncelikle belirlenen aralık olan (0 \leq x \leq 1) için (f(x)) değerlerini hesaplarız.

1. Fonksiyon Değerleri:

   • (x = 0) için (f(0) = 2(1-0) = 2)
   • (x = 0.5) için (f(0.5) = 2(1-0.5) = 1)
   • (x = 1) için (f(1) = 2(1-1) = 0)

2. Grafiğin Özellikleri:

   • Grafiğin en yüksek noktası ( (0, 2) )'dir.
   • Grafiğin x eksenini kestiği nokta ( (1, 0) )'dir.
   • Aralık dışında ( f(x) = 0 ) olduğu için burada herhangi bir nokta yoktur.

Yukarıdaki bilgileri kullanarak grafiği çizmek için aşağıdaki kodu kullanabilirsiniz:

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(-0.5, 1.5, 100)
f_x = np.where((x >= 0) & (x <= 1), 2 * (1 - x), 0)

plt.plot(x, f_x, label='f(x) = 2(1-x)', color='blue')
plt.title('Olasılık Yoğunluk Fonksiyonu f(x)')
plt.xlabel('x')
plt.ylabel('f(x)')
plt.axhline(0, color='black', lw=0.5, ls='--')
plt.axvline(0, color='black', lw=0.5, ls='--')
plt.xlim([-0.5, 1.5])
plt.ylim([-0.5, 2.5])
plt.fill_between(x, f_x, color='blue', alpha=0.1)
plt.legend()
plt.grid()
plt.show()

b) Toplam Dağılım Fonksiyonu F(x)

Toplam dağılım fonksiyonu, olasılık yoğunluk fonksiyonunun integralidir. Yani:

F(x) = \int_{-\infty}^{x} f(t) dt

F(x) Fonksiyonunun Hesaplanması:

• ( x < 0 ) için:

  • ( F(x) = 0 ) (çünkü f(x) = 0)

• ( 0 \le x < 1 ) için:

  F(x) = \int_0^{x} 2(1-t) dt = 2 \left[ t - \frac{t^2}{2} \right]_0^{x} = 2 \left[ x - \frac{x^2}{2} \right] = 2x - x^2

• ( x \ge 1 ) için:

  F(x) = 1 \quad (\text{çünkü tüm olasılık 1'e kadar toplanmış olur})

Böylece toplam dağılım fonksiyonu:

F(x) = \begin{cases} 0 & \text{eğer } x < 0 \\ 2x - x^2 & \text{eğer } 0 \leq x < 1 \\ 1 & \text{eğer } x \geq 1 \end{cases}

Grafiğin Çizimi:

F(x) fonksiyonunu çizmek için aynı şekilde bir grafik oluşturabilirsiniz:

x = np.linspace(-0.5, 2, 100)
F_x = np.where(x < 0, 0, np.where(x < 1, 2*x - x**2, 1))

plt.plot(x, F_x, label='F(x)', color='orange')
plt.title('Toplam Dağılım Fonksiyonu F(x)')
plt.xlabel('x')
plt.ylabel('F(x)')
plt.axhline(0, color='black', lw=0.5, ls='--')
plt.axvline(0, color='black', lw=0.5, ls='--')
plt.xlim([-0.5, 2])
plt.ylim([-0.1, 1.1])
plt.legend()
plt.grid()
plt.show()

Sonuç

Düzenlediğimiz bu bilgiler ışığında, verilen sürekli rassal değişkenin olasılık yoğunluk fonksiyonu grafiği ve toplam dağılım fonksiyonu hesaplanmış ve çizilmiştir. Bu tür hesaplamalar, istatistiksel analizlerde olayların olasılığını daha iyi anlamamıza yardımcı olmaktadır.

Görüntü oluştur

continuous probability function, f(x) = 2(1-x) for 0 <= x <= 1, x-axis 0 to 1, y-axis 0 to 2, linear decreasing graph

TERİMLER:

Olasılık Yoğunluk Fonksiyonu: Bir sürekli rassal değişkenin olasılıklarını tanımlayan fonksiyon.
Toplam Dağılım Fonksiyonu: Bir değişkenin belirli bir değerin altında kalma olasılığını ifade eden fonksiyon.