Doğru cevap: C) 6
1. Sorunun Çözümü
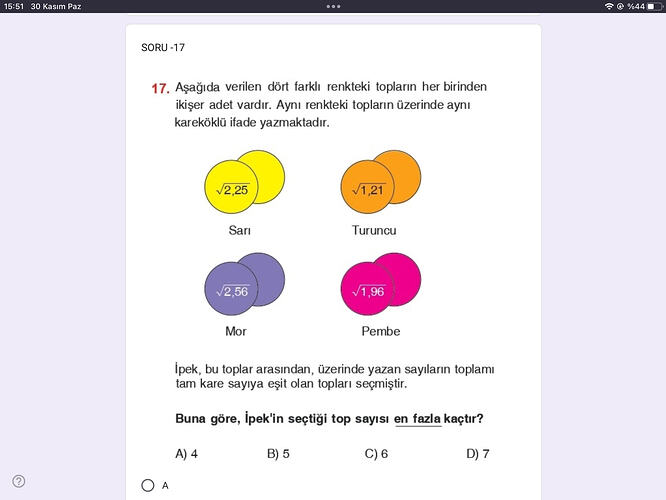
Her renkten 2’şer tane top var ve aynı renkteki topların üstünde aynı sayı yazıyor:
- Sarı toplar: \sqrt{2{,}25}
- Turuncu toplar: \sqrt{1{,}21}
- Mor toplar: \sqrt{2{,}56}
- Pembe toplar: \sqrt{1{,}96}
Önce bu köklü sayıları karelerini alarak sadeleştirelim:
- 2{,}25 = \frac{9}{4} = \left( \frac{3}{2} \right)^2 \Rightarrow \sqrt{2{,}25} = \frac{3}{2}
- 1{,}21 = \frac{121}{100} = \left( \frac{11}{10} \right)^2 \Rightarrow \sqrt{1{,}21} = \frac{11}{10}
- 2{,}56 = \frac{256}{100} = \left( \frac{16}{10} \right)^2 = \left( \frac{8}{5} \right)^2 \Rightarrow \sqrt{2{,}56} = \frac{8}{5}
- 1{,}96 = \frac{196}{100} = \left( \frac{14}{10} \right)^2 = \left( \frac{7}{5} \right)^2 \Rightarrow \sqrt{1{,}96} = \frac{7}{5}
Yani toplardaki değerler:
- Sarı: \frac{3}{2}
- Turuncu: \frac{11}{10}
- Mor: \frac{8}{5}
- Pembe: \frac{7}{5}
Her renkten en fazla 2 top alabiliriz.
İpek, seçtiği topların üzerindeki sayıların toplamı tam kare olsun istiyor ( 1,4,9,16,\dots gibi).
2. Tüm topları 2’şer 2’şer almayı deneyelim
En fazla top sayısını bulmak için önce hepsini alırsak ne olur, bakalım:
- 2 sarı top: 2 \cdot \frac{3}{2} = 3
- 2 turuncu top: 2 \cdot \frac{11}{10} = \frac{22}{10} = 2{,}2
- 2 mor top: 2 \cdot \frac{8}{5} = \frac{16}{5} = 3{,}2
- 2 pembe top: 2 \cdot \frac{7}{5} = \frac{14}{5} = 2{,}8
Toplam:
3 + 2{,}2 + 3{,}2 + 2{,}8 = 11{,}2
Kesirli olarak:
3 = \frac{30}{10},\; 2{,}2 = \frac{22}{10},\; 3{,}2 = \frac{32}{10},\; 2{,}8 = \frac{28}{10}
\frac{30}{10} + \frac{22}{10} + \frac{32}{10} + \frac{28}{10}
= \frac{112}{10} = \frac{56}{5} = 11{,}2
\frac{56}{5} bir tam kare değil.
Ama dikkat: Tüm terimlerin paydasını 10 yaparsak daha rahat kombinasyon deneriz.
3. Hepsini ortak paydada yazalım
- \frac{3}{2} = \frac{15}{10}
- \frac{11}{10} = \frac{11}{10}
- \frac{8}{5} = \frac{16}{10}
- \frac{7}{5} = \frac{14}{10}
Her renkten en fazla 2 top:
- 2 sarı: 2 \cdot \frac{15}{10} = \frac{30}{10}
- 2 turuncu: 2 \cdot \frac{11}{10} = \frac{22}{10}
- 2 mor: 2 \cdot \frac{16}{10} = \frac{32}{10}
- 2 pembe: 2 \cdot \frac{14}{10} = \frac{28}{10}
Hepsinin toplamı:
\frac{30 + 22 + 32 + 28}{10} = \frac{112}{10} = \frac{56}{5}
İpek’in alacağı topların toplamı \frac{n}{10} şeklinde olacak, çünkü tüm sayıların paydası 10 .
Tam kare olması için:
\frac{n}{10} = k^2 \Rightarrow n = 10k^2
Yani n sayısı 10’un katı olmalı.
Bizim elimizdeki her bir topun değeri (pay kısmı):
- Sarı top: 15
- Turuncu top: 11
- Mor top: 16
- Pembe top: 14
Toplamda kullanabileceğimiz en büyük pay:
2\cdot 15 + 2\cdot 11 + 2\cdot 16 + 2\cdot 14 = 112
Dolayısıyla n \le 112 ve n = 10k^2 .
Uygun k^2 değerleri:
k^2 = 1,4,9 için 10,40,90 (çünkü 10\cdot 16 =160>112 ).
En büyüğü 90 .
Yani topların pay toplamını 90 yapabilirsek, toplam:
\frac{90}{10} = 9
olur, bu da tam kare.
4. Pay toplamı 90 olacak kombinasyonu bulalım
Maksimum top sayısını istiyoruz, o yüzden 8 top (hepsi) mümkün mü diye kontrol edelim:
- 8 topun pay toplamı: 112
- 112, 10’un katı değil ⇒ olmaz.
Sonraki en yüksek adet: 7 top.
7 top seçersek, 1 top dışarıda kalır. Dışarıda kalan topun payları olabilir: 15, 11, 16, 14 .
112’den bu değerleri çıkaralım:
- 112 − 15 = 97 (10’un katı değil)
- 112 − 11 = 101 (10’un katı değil)
- 112 − 16 = 96 (10’un katı değil)
- 112 − 14 = 98 (10’un katı değil)
Hiçbiri 10k^2 şeklinde değil ⇒ 7 top mümkün değil.
Şimdi 6 top deneyelim. 2 topu dışarıda bırakacağız.
Çıkardığımız 2 topun payları (aynı renkten veya farklı olabilir) ve kalan toplam:
- 15 + 11 = 26 \Rightarrow 112 - 26 = 86
- 15 + 16 = 31 \Rightarrow 112 - 31 = 81
- 15 + 14 = 29 \Rightarrow 112 - 29 = 83
- 11 + 16 = 27 \Rightarrow 112 - 27 = 85
- 11 + 14 = 25 \Rightarrow 112 - 25 = 87
- 16 + 14 = 30 \Rightarrow 112 - 30 = 82
Ayrıca aynı renkten ikişer topu çıkarma durumları:
- 2\cdot 15 = 30 \Rightarrow 112 - 30 = 82
- 2\cdot 11 = 22 \Rightarrow 112 - 22 = 90
- 2\cdot 16 = 32 \Rightarrow 112 - 32 = 80
- 2\cdot 14 = 28 \Rightarrow 112 - 28 = 84
Bunlardan sadece 8. durumda:
112 - 22 = 90
elde ediyoruz.
Yani 2 turuncu topu hiç seçmeyip diğer 6 topu (2 sarı, 2 mor, 2 pembe) alırsak, pay toplamı 90 olur.
Toplam değer:
2\cdot \frac{3}{2} + 2\cdot \frac{8}{5} + 2\cdot \frac{7}{5}
= 3 + \frac{16}{5} + \frac{14}{5}
= 3 + \frac{30}{5}
= 3 + 6
= 9
9 bir tam kare olduğu için şartı sağlıyor.
Dolayısıyla İpek’in seçebileceği en fazla top sayısı 6’dır.
Sonuç
İpek en fazla 6 top seçebilir.
Cevap: C) 6
TERİMLER:
Tam kare: Bir tam sayının karesi olan sayılar. Örneğin 1,4,9,16,25,\dots gibi.
Karekök ( \sqrt{\ \ } ): Karesi verilen sayıyı veren işlem. Örneğin \sqrt{9} = 3 çünkü 3^2 = 9 .