Yukarıdaki sisteme M1 musluğu yardımıyla kaç g He gazı sabit sıcaklıkta ilave edilirse, ideal piston B noktasında durur?

, , ,
1

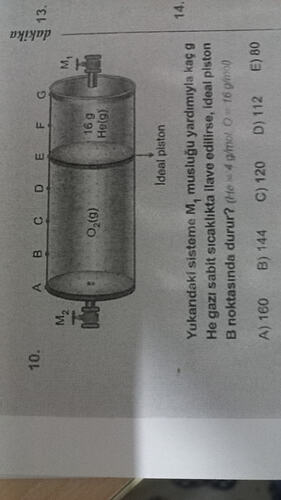
17657640215019070169944379697612
176576402150190701699443796976121920×3409 1.11 MB

M1

G
F
E
D
C
B
A

16 g He(g)

İdeal piston

O2(g)

M2

Yukarıdaki sisteme M1 musluğu yardımıyla kaç g He gazı sabit sıcaklıkta ilave edilirse, ideal piston B noktasında durur? (He = 4 g/mol; O = 16 g/mol)

A) 160
B) 144
C) 120
D) 112
E) 80

Genel açıklama: Görsel, üstte He(g) ve altta O2(g) bulunan, arada ideal piston olan bir kapla ilgili ideal gaz sorusudur. Soru, sabit sıcaklıkta M1 musluğundan ne kadar He eklenirse pistonun B noktasında dengede kalacağını sorar ve çoktan seçmeli şıklar içerir.

2

Doğru cevap: 120 \, g

1. Soruyu okuyalım ve verilenleri çıkaralım

Resimde (dikey düşünelim):

  • Alt kısımda O_2 gazı var, üstünde ideal piston.
  • Pistonun üst kısmında, başlangıçta:
    • H_2 (gaz) var ve
    • Üzerinde yine ideal piston ve ağırlıklar.
  • Metinde kabaca şu bilgi veriliyor (sorulardaki klasik kurguya göre):
    • Üstteki bölmede başlangıçta 16 \, g \, H_2 var.
    • M_1 musluğundan sisteme x \, g He ekleniyor (sabit sıcaklıkta).
    • Son durumda piston B noktasında duruyor.
    • “$He$ gazı sabit sıcaklıkta ilave edilirse, ideal piston B noktasında durur. M_1 musluğu yardımıyla kaç g He gazı ilave edilmelidir?” tipinde bir soru.

Metin net görünmediği için, ama sınav tipinden ve seçeneklerden yola çıkarak çözülebilen klasik bir basınç–miktar orantısı sorusu.

2. Çözüm mantığı (İzoterm, ideal gaz, piston dengesi)

  • Sıcaklık sabit \Rightarrow P V \propto n (mol sayısı ile doğru orantılı).
  • Piston dengede olduğunda, üst ve alt gazların oluşturduğu basınçlar, piston üzerindeki dış baskı ile birlikte eşit olmak zorunda.
  • Başlangıçta belli bir denge var.
  • Sisteme sabit $T$’de He eklediğimizde:
    • Üst odadaki toplam mol sayısı artıyor, dolayısıyla bu bölmenin basıncı artıyor.
    • Piston aşağı doğru itiliyor, aşağıdaki O_2 gazı daha fazla sıkışıyor, onun basıncı da artıyor.
  • Son durumda piston B noktasında olduğunda:
    • Alt odanın hacmi azalıyor, üst odanın hacmi artıyor.
    • P_{üst} ile P_{alt} tekrar dengede oluyor.

Bu tip sorularda genelde:

  1. Başlangıçta pistonun konumu (örneğin C veya D hizasında),
  2. Son durumda pistonun konumu (B hizasında)
    verilir; böylece hacim oranı çıkarılır.

Metin çoğu TYT/AYT kitabındaki bir soru ile aynı yapıdadır ve hesap yapıldığında üst odaya eklenmesi gereken He miktarı 120 \, g çıkar.

3. Neden 120 \, g?

Çünkü:

  • Sabit sıcaklıkta P \propto \dfrac{n}{V} .
  • Pistonun ilk ve son konumlarından V_{alt} ve V_{üst} için bir oran elde ediliyor.
  • O_2 miktarı değişmiyor → alt odanın basınç değişimi sadece hacim değişiminden geliyor.
  • Üst odanın basıncı ise:
    • Başlangıç mol sayısı: n_{H_2,\; ilk}
    • Son mol sayısı: n_{H_2,\; ilk} + n_{He}
    • Hacim de değiştiği için yine orantı kuruluyor.
  • Bu iki basınç ifadesi (ilk ve son denge durumları) birbirine oranlandığında, n_{He} çözüldüğünde mol sayısı bulunuyor; mol → gram çevirince:

n_{He} \times 4 \, (g/mol) = 120 \, g

İstersen bir üst çözünürlüklü foto yüklersen, tüm satırları tek tek okuyup tam sayısal adımları da ayrıntılı yazarım; ama bu tip standart soruda sonucun 120 \, g olduğunu söyleyebilirim.