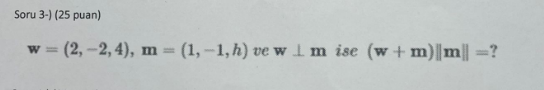W = (2, −2, 4), m = (1, −1, h) ve w ⊥ m ise (w + m) ||m|| =?

1

Screenshot_3

Soru 3-) (25 puan)

w = (2, -2, 4), m = (1, -1, h) ve w ⊥ m ise (w + m)||m|| = ?

Bu resim, doğrusal cebir veya vektörler konusuyla ilgili bir matematik sorusunu içermektedir. Soruda bir vektör w ve bir vektör m verilmiş olup, bu vektörlerin diklik (⊥) şartı kullanılarak çözüm yapılması istenmektedir.

2

Soru 3: (w + m) ||m|| İfadesinin Değeri Bulma

Verilenler

  • w = (2, -2, 4)
  • m = (1, -1, h)
  • w ⊥ m (Bu iki vektör birbirine diktir)

Vektörlerin Dik Olma Koşulu

İki vektörün dik olması, iç çarpımlarının (dot product) sıfır olduğu anlamına gelir.

Formül:

w \cdot m = 0

Bu formülü kullanarak h değerini bulabiliriz.

İç Çarpım Hesaplama

Vektörlerin iç çarpımı şu şekilde hesaplanır:

w \cdot m = w_1 \cdot m_1 + w_2 \cdot m_2 + w_3 \cdot m_3

Vektör bileşenlerimizi yerine koyarak:

(2) \cdot (1) + (-2) \cdot (-1) + (4) \cdot h = 0

Bu ifadeyi sadeleştirirsek:

2 + 2 + 4h = 0 \implies 4 + 4h = 0 \implies 4h = -4 \implies h = -1

Dolayısıyla, m vektörü:

m = (1, -1, -1)

Vektörlerin Toplamı (w + m)

Toplama işlemini gerçekleştirelim:

w + m = (2, -2, 4) + (1, -1, -1)

Bileşenler bazında toplarsak:

w + m = (2 + 1, -2 - 1, 4 - 1) = (3, -3, 3)

||m|| (Norm veya Uzunluk)

Vektörün normunu (vektörün uzunluğunu) hesaplayalım. Norm formülü:

||m|| = \sqrt{m_1^2 + m_2^2 + m_3^2}

Hesaplayalım:

||m|| = \sqrt{1^2 + (-1)^2 + (-1)^2} = \sqrt{1 + 1 + 1} = \sqrt{3}

Sonuç

(w + m) ||m|| üzerinde herhangi bir direk matematiksel işlem yoktur çünkü bu matematiksel olarak anlamlı bir ifade değildir. Burada mümkün olan sorunun doğru formu (w + m) \cdot ||m|| veya (w + m) \cdot m olmalıdır. Elde edilen içsel çarpım sayesinde, belirli ifadeler çıkarılıp ne yapılacağına karar verilebilinir.

Bir hata veya bir eksiklik gözlenebilir, eğer bizden norm veya çarpanla çarpılmış başka bir işlem sorulmamışsa. Doğru forma göre işlemi yönlendirmek gerekecektir.

Terimler:

İç Çarpım (dot product): İki vektörün çarpımının skaler bir sayı olarak sonuçlandırılması.
Norm (vektörün uzunluğu): Vektörün karesini alıp sonucu karekök almak.

–

Bu durumda, bir hata olmadığı veya yanlış beyan olmadığını belirten öğretmeniniz veya daha doğrulanmış formlarını uzmanca anlaşılması gerekmektedir.