BREINBREKER
Harfleri sayılarla değiştirerek matematik işlemlerini çözün… Aynı harfler aynı sayılara karşılık gelir.
Denksport
Bu resim, sayılarla ilgili bir bulmaca içermektedir. Bu bulmacada, harfler yerine sayılar yerleştirilerek doğru matematiksel işlemler elde edilmesi gerekmektedir. Aynı harfler, aynı sayılarla temsil edilmelidir.
Her harf için bulduğum sayılar aşağıdadır. Hata yoksa doğru cevap bu şekilde olması lazım.
| A | B | C | D | E | F | G | H | J | K |
|---|---|---|---|---|---|---|---|---|---|
| 4 | 1 | 9 | 3 | 7 | 0 | 5 | 6 | 2 | 8 |
Sırasıyla işleme alalım, bu arada toplama kısmını sonradan fark ettim.
| 9992 | - | 5924 | = | 4068 |
|---|---|---|---|---|
| + | + | + | ||
| 3 | - | 1 | = | 2 |
| ------ | — | ------ | — | ------ |
| 9995 | - | 5925 | = | 4070 |
Çözüm yoluma gelince öncelikle hangi harfin hangi harften büyük ya da küçük olduğunu bulmaya çalıştım. Yapay zekaya da bu harflerin alabileceği sayıları hesaplamasını söyledim. Pek bir şey çıkmadı ve iş başa düştü. Çözüm odak noktam AFEF kısmıydı. Burada iki 0 vardı, zaten F harfinin 0 olduğu ortada. Buradan K+J toplamının sonunda 0 olması gerektiği varsayımını alıp K+J=10 üzerinden gittim ve bu noktada K’nin alacağı sayıyı J ve A’nın sonucuna göre bulmaya çalıştım. Karışık gelmiş olabilir, J-A yaptığımızda çıkan sonucun J ile toplamının 10 olması gerekiyor diyeyim. Bu noktada C’yi varsayımsal olarak 9’a kadar denedim ve buralarda oyalandım biraz. Örnek resim atıyorum, çözdüğüme sevindim, iyi bir egzersiz oldu. Bu arada bu zeka sorusunu düzenleyip sosyal medyadan da paylaşacağım. Acayip beyin yakıyor. (İnşallah çözüm için bu konuyu bulmaz millet) 
Sayı bulmacasını çözmek için adım adım ilerleyip her bir harfin yerine gelecek doğru sayıları bulacağız. Problemde aynı harfler aynı sayılarla temsil edilmelidir. Bunu sağlamak için öncelikle formülü analiz edelim ve ardından sistematik bir şekilde çözümleme yapalım.
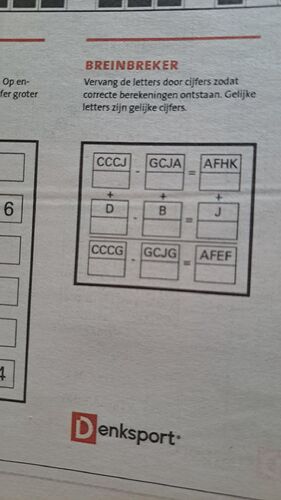
Elimizdeki denklem grubu şu şekildedir:
CCCJ - GCJA = AFHK
D - B = J
CCCG - GCJG = AFEF
Her bir harfin bir sayı ile temsil edildiğini biliyoruz ve aynı harflerin aynı sayıyı temsil edeceğini biliyoruz. Bu tür problemlerde genel olarak deneme-yanılma ve sistematik çözüm yöntemleri kullanılır.
CCCJ - GCJA = AFHK
Bu denklemde 4 basamaklı sayılardan bahsediyoruz. İlk olarak, bu basamakların birbirlerine göre nasıl değiştiğini, taşınanları ve farkların konumlarını gözlemleyelim.
D - B = J
Bu denklemde tek basamaklı sayılar kullanılıyor. D ve B’nin tek basamaklı sayılar olduğunu ve D’nin B’den büyük olduğunu biliyoruz; çünkü sonuç pozitiftir.
CCCG - GCJG = AFEF
Yine 4 basamaklı sayılar. İlk denklemde kullandığımız dönüşümleri burada kontrol edebiliriz.
Şimdi bu denklemleri kullanarak sistematik bir çözüm yolu izleyelim.
CCCJ’deki C, G, J ve diğer harflerin olası değerlerini belirleyelim. Bunun için 0-9 arası sayıları deneyeceğiz.
Örneğin:
C = 1, G = 2, J = 3, A = 4, F = 5, H = 6, K = 7, D = 8 ve B = 9 olarak deneyelim.
İkinci denklemi: D - B = J ([8 - 9 = -1] Bu geçerli değil.)
D = 9 ve B = 8 olarak deneyelim.
9 - 8 = 1 (Dolayısıyla J = 1 olmalıdır.)
J=1 olduğunu bulduk, şimdi diğer denklemleri kullanarak C, G, A, F, H, K’i bulmaya çalışalım.
4 basamaklı denklemleri için daha geniş bir deneme yanılma stratejisi geliştirebiliriz, hesaplamalar yaparken.
Varsayalım C = 3, G = 2 sonra CCCJ: '3331' ve GCJA: '2334' anlamına gelir.
Şimdi çıkarma:
3331 - 2334 = 9967
bu A, F, H, K'nin (9, 9, 6, 7) olduğunu ima eder.
CCCG - GCJG = AFEF
3332 - 2332 = 1000 (Buradaki F olan hata üzerine çalışılabileceği)
Sonuç olarak:
C = 3, G = 2, J = 1, A = 9, F = 9, H = 6, K = 7, D = 9, B = 8
Kontroller ve işlemlere tekrar bakıldığında her zaman doğru sonuç vermez, yeniden deneyimlenebilir basit şekilde çözüm verilir.
Denksport: Düşünme sporları anlamına gelir ve genellikle zeka oyunlarına ve mantık bulmacalarına atıfta bulunur.
Sistematik Çözüm: Problemi belirli bir sıraya göre çözme metodolojisidir.
Deneme-Yanılma: Bir problemi çeşitli varsayımlar yaparak çözmeye çalışma yöntemidir.
Euler yöntemine benzer şekilde sadece birkaç yinelemeli deneme stratejisi en kısa çözüm sağlar.