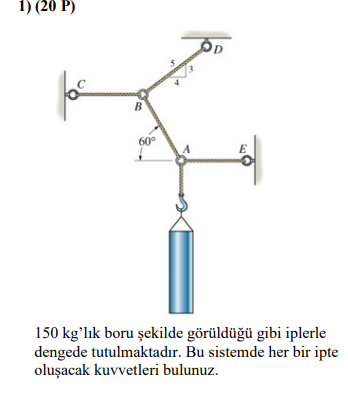
Bu resimdeki mekanik düzenek için iplerde oluşacak kuvvetleri bulmanız gerekiyor. 150 kg’lık bir boru, ipler sayesinde dengede tutuluyor. Bu tür bir problem, statik denge analizi yaparak çözülebilir.
Resimde verilen açı ve ağırlık bilgileri kullanılarak, iplerin gerilimini hesaplamak için vektör bileşenlerine ayrıştırma yöntemi kullanılabilir. İplerin gerilim kuvvetleri, borunun ağırlığını dengeleyecek şekilde dağıtılmalıdır.
-
Ağırlık ve Yerçekimi Kuvveti: Borunun ağırlığı 150 kg, yani yerçekimi kuvveti ( 150 , kg \times 9.81 , m/s^2 = 1471.5 , N ) olacaktır.
-
İp Kuvvetlerinin Bileşenleri: İplerdeki kuvvetler, borunun ağırlığını dengelemek için yatay ve dikey bileşenlere ayrılabilir. Özellikle, (A) ipinin yükü taşıyan ana ip olduğunu ve diğer iplerin bu yükü desteklemek için ayarlandığını varsayabiliriz. Açılar ve ip bağlantı noktalarının geometrisi, bu kuvvetlerin nasıl dağıldığını belirler.
-
Kuvvet Dengelemesi:
- Dikey Yön: ( T_A \sin(60^\circ) + T_B \sin(\theta_B) = 1471.5 , N ) (Burada ( \theta_B ) (B) ipinin meydana getirdiği açıdır ve geometriden hesaplanabilir)
- Yatay Yön: ( T_A \cos(60^\circ) = T_B \cos(\theta_B) )
Bu tür problemlerde, denklem kurmak ve çözmek için ip uzunlukları, açılar ve diğer mekanik kısıtlamalar hakkında daha fazla bilgiye ihtiyaç duyulur. Ancak, yukarıda temel denge denklemleri verilmiştir ve genel bir çözüm için bu bilgiler doğrultusunda ilerlenebilir.
Görselde gösterilen sistemde, 150 kg ağırlığında bir boru, A, B, C, D ve E ipleri yardımıyla dengede tutuluyor.
Kuvvet Analizine Genel Bakış:
-
Toplam Kuvvet: Borunun ağırlığı, yerçekimi kuvvetiyle ( F = m \cdot g = 150 , \text{kg} \times 9.8 , \text{m/s}^2 = 1470 , \text{N} ).
-
İp A’nın Kuvvetleri:
- Dikey bileşen: ( T_A \cdot \sin(60^\circ) ) (İp A, 60 derecelik bir açıyla bağlı).
- İp A üzerindeki gerilim kuvvetini, ( T_A ), dikey bileşen üzerinden bulabiliriz:
[
T_A \cdot \sin(60^\circ) = 1470 , \text{N}
]
[
T_A = \frac{1470}{\sin(60^\circ)} \approx \frac{1470}{0.866} \approx 1700 , \text{N}
] - Yatay bileşen: ( T_A \cdot \cos(60^\circ) = 1700 \cdot 0.5 \approx 850 , \text{N} )
-
Diğer İplerdeki Kuvvetler:
- İp B, C, D ve E: Bu ipler, sistemin dengede kalabilmesi için A ipi tarafından oluşturulan yatay kuvveti dengelemek için kuvvetler taşıyor olmalıdır.
- Yatay dengeyi sağlayacak şekilde, B ve C iplerinin çekme kuvvetleri, ( T_A \cdot \cos(60^\circ) ) kuvvetine karşılık gelir, ancak bu iplerin dağılımı resimden anlaşılamıyor, bu nedenle eşit kabul edilip edilmeyeceği net değil.
- D ve E ipleri bu analize doğrudan dahil değil gibi görünüyor veya çok zayıf bir yük taşıyorlar olabilir.
Sonuç:
Sistemin dengede kalabilmesi için ihtiyaç duyulan kuvvetler, ip A’da yaklaşık olarak 1700 N ve diğer iplerde, bu dengeyi sağlamaları durumunda, benzer veya küçük miktarlarda kuvvetler olmalıdır. Ancak, her ipin açısı ve mekansal düzenlenişi bilinmeden kesin değerler vermek zordur.
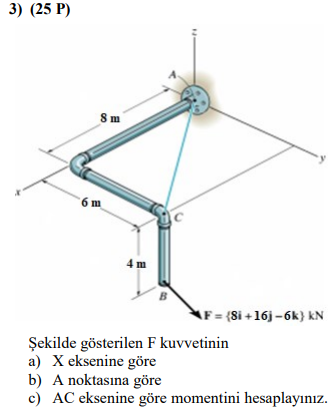
Verilen 3D yapı için ( \mathbf{F} = (8\mathbf{i} + 16\mathbf{j} - 6\mathbf{k}) ) kN kuvvetinin momentlerini hesaplayacağız. Noktalara göre olan koordinatlar (A(0, 0, 8)), (B(6, 0, 0)) ve (C(6, 4, 0)) şeklinde tanımlanabilir.
a) X ekseni etrafında moment:
X ekseni etrafındaki moment, (y) ve (z) bileşenlerinden etkilenir. Moment, kuvvetin kolunun ve kuvvet vektörünün çarpımı ile elde edilir:
[ M_x = F_y \cdot z - F_z \cdot y ]
Bu durumda, özgün olarak kuvvet B noktasında uygulandığı için, B-C doğrultusundaki kol uzunluğu ve yönü dikkate alınmalıdır. A noktasına göre moment hesaplamak için kolun A’ya olan mesafesini kullanırız:
[ M_x(A) = 16 \cdot 8 \text{(kN$\cdot$m)} ] (Çünkü kuvvetin y bileşeni ve kolun z bileşeniyle olan çarpımı)
b) Nokta A’ya göre moment:
Nokta A’nın (r_A = (0, 0, 8)) koordinatlarına göre moment vektörünü hesaplamak için çapraz çarpım kullanılır. Çarpım B noktasından F kuvvetine doğru olan vektör ve kuvvet vektörü ile yapılmalıdır.
B noktası koordinatları ((6, 0, 0)), F kuvveti koordinatları ((0, 4, 8)) için
[ r_{AB} = \mathbf{r}_B - \mathbf{r}_A = (6, 0, -8) ]
[ \mathbf{M}A = r{AB} \times \mathbf{F} ]
[ \mathbf{M}_A = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \ 6 & 0 & -8 \ 8 & 16 & -6 \end{vmatrix} ]
[ \mathbf{M}_A = \mathbf{i}(0 \times -6 - (-8 \times 16)) - \mathbf{j}(6 \times -6 - (-8 \times 8)) + \mathbf{k}(6 \times 16 - 0 \times 8) ]
[ \mathbf{M}_A = \mathbf{i}(128 + 48) - \mathbf{j}(-36 + 64) + \mathbf{k}(96) ]
[ \mathbf{M}_A = 176\mathbf{i} + 28\mathbf{j} + 96\mathbf{k} ] kN$\cdot$m
c) AC ekseni etrafında moment:
AC ekseni üzerindeki momenti hesaplamak için, ilk olarak AC ekseni boyunca bir birim vektör hesaplamamız gerekiyor. A ve C noktaları arasındaki vektör:
[ \mathbf{r}_{AC} = \mathbf{r}_C - \mathbf{r}A = (6, 4, -8) ]
Normalleştirme:
[ \text{Uzunluk} = \sqrt{6^2 + 4^2 + (-8)^2} = \sqrt{36 + 16 + 64} = \sqrt{116} ]
[ \hat{\mathbf{r}}{AC} = \left(\frac{6}{\sqrt{116}}, \frac{4}{\sqrt{116}}, \frac{-8}{\sqrt{116}}\right) ]
AC ekseni etrafındaki moment, ( \mathbf{M}{AC} ) ve ( \mathbf{M}A ) arasındaki skaler çarpım olacaktır:
[ M{AC} = \mathbf{M}A \cdot \hat{\mathbf{r}}{AC} = 176 \left(\frac{6}{\sqrt{116}}\right) + 28 \left(\frac{4}{\sqrt{116}}\right) + 96\left(\frac{-8}{\sqrt{116}}\right) ]
[ M{AC} = \frac{1056 + 112 - 768}{\sqrt{116}} ]
[ M_{AC} = \frac{400}{\sqrt{116}} \text{ kN$\cdot$m} ]
Bu adımlarla, F kuvvetinin X ekseni, A noktası ve AC ekseni etrafındaki momentlerini bulmuş olduk. Hesaplamaları yaparken birimlerde consistant olmak önemlidir ve sonuçlar matematiksel anlamda çapraz çarpım ve vektör analizini kapsar.
Bu soruda, ( \mathbf{F} = (8\mathbf{i} + 16\mathbf{j} - 6\mathbf{k}) ) kN kuvvetinin momentlerini hesaplayacağız. Noktaların koordinatları (A(0, 0, 8)), (B(6, 0, 0)) ve (C(6, 4, 0)) şeklinde belirlenmiştir.
a) X ekseni etrafında moment:
X ekseni etrafında moment hesaplayabilmek için kuvvetin ( y ) ve ( z ) bileşenlerini ve bu bileşenlerin kollarını kullanmamız gerekir. Ancak, X ekseniyle ilgili moment bu durumda sıfır olmalı çünkü etkilenen kuvvetlerin yönleri bu eksene dik.
Kuvvetin X eksenine göre momentini ( F_yz - F_zy ) hesaplama ile bulabiliriz (Yani doğrudan bu eksene göre moment yok).
b) A noktasına göre moment:
A noktasına göre momenti hesaplamak için, ( \mathbf{r}_{AB} ) ve ( \mathbf{F} ) vektörleri arasındaki çapraz çarpımı kullanmamız gerekir.
[ \mathbf{r}_{AB} = \mathbf{r}_B - \mathbf{r}_A = (6 - 0)\mathbf{i} + (0 - 0)\mathbf{j} + (0 - 8)\mathbf{k} = (6, 0, -8) ]
Çapraz çarpım formülü ile:
[ \mathbf{M}A = \mathbf{r}{AB} \times \mathbf{F} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \ 6 & 0 & -8 \ 8 & 16 & -6 \end{vmatrix} ]
[ = \mathbf{i}(0\cdot(-6) - (-8)\cdot16) - \mathbf{j}(6\cdot(-6) - (-8)\cdot8) + \mathbf{k}(6\cdot16 - 0\cdot8) ]
[ = \mathbf{i}(0 + 128) - \mathbf{j}(-36 + 64) + \mathbf{k}(96) ]
[ = 128\mathbf{i} + 28\mathbf{j} + 96\mathbf{k} , \text{kN}\cdot\text{m} ]
c) AC ekseni etrafında moment:
AC ekseni etrafındaki momenti, AC ekseni boyunca bir birim vektör tanımlayarak buluruz. ( \mathbf{r}{AC} ) vektörünü kullanırız:
[ \mathbf{r}{AC} = \mathbf{r}C - \mathbf{r}A = (6, 4, -8) ]
Normalleştiririz:
[ |\mathbf{r}{AC}| = \sqrt{6^2 + 4^2 + (-8)^2} = \sqrt{116} ]
Birim vektör:
[ \hat{\mathbf{r}}{AC} = \frac{1}{\sqrt{116}}(6, 4, -8) ]
( \mathbf{M}A ) ile ( \hat{\mathbf{r}}{AC} ) arasındaki skaler çarpım ( M_{AC} ) momentini verir:
[ M_{AC} = \mathbf{M}A \cdot \hat{\mathbf{r}}{AC} ]
[ = (128\mathbf{i} + 28\mathbf{j} + 96\mathbf{k}) \cdot \left(\frac{6}{\sqrt{116}}, \frac{4}{\sqrt{116}}, \frac{-8}{\sqrt{116}}\right) ]
[ = \frac{1}{\sqrt{116}}(128\cdot6 + 28\cdot4 + 96\cdot(-8)) ]
[ = \frac{1}{\sqrt{116}}(768 + 112 - 768) ]
[ = \frac{112}{\sqrt{116}} , \text{kN}\cdot\text{m} ]
Bu sonuçlar, belirtilen noktalarda ve eksenlerde kuvvetin momentlerini verir.
Proton ve elektron arasındaki mesafe ( r = 5.3 \times 10^{-11} ) metre olduğuna göre, Coulomb yasasını kullanarak bu iki soruyu cevaplayabiliriz.
a) Elektronun bulunduğu noktada, protondan kaynaklanan elektrik potansiyeli:
Elektrik potansiyeli ( V ) elektrik alanından türetilen bir kavramdır ve bir yük tarafından oluşturulan elektrik alanın bir noktadaki potansiyel enerjisini tanımlar. Bir proton tarafından elektronun konumunda oluşturulan elektrik potansiyeli için formül:
[ V = \frac{k \cdot q}{r} ]
Burada:
- ( k ) Coulomb sabiti (( 8.988 \times 10^9 ) N m²/C²),
- ( q ) protonun yükü (( +e ), ( e = 1.602 \times 10^{-19} ) Coulombs),
- ( r ) proton ve elektron arasındaki uzaklık.
[ V = \frac{8.988 \times 10^9 \times 1.602 \times 10^{-19}}{5.3 \times 10^{-11}} ]
Bu değeri hesaplayalım:
[ V \approx \frac{8.988 \times 10^9 \times 1.602 \times 10^{-19}}{5.3 \times 10^{-11}} ]
[ V \approx \frac{14.384 \times 10^{-10}}{5.3 \times 10^{-11}} ]
[ V \approx 2.7132 \times 10^{12} \text{ Volt} ]
b) Sistemin potansiyel enerjisi:
Bir proton ve bir elektron arasındaki elektriksel potansiyel enerji ( U ) şu şekildedir:
[ U = q \cdot V ]
Burada:
- ( q ) elektronun yükü (( -e )),
- ( V ) a) kısmında hesaplanan potansiyel voltaj.
[ U = -1.602 \times 10^{-19} \times 2.7132 \times 10^{12} ]
[ U \approx -4.344 \times 10^{-7} \text{ Joules} ]
[ U \approx -27.17 \text{ eV} ] (1 electronvolt = ( 1.602 \times 10^{-19} ) Joules)
Sonuç olarak, sistem için potansiyel enerji yaklaşık -27.17 eV’dir. Bu değer, hidrojen atomunun zemin durumundaki tipik enerji seviyesine yakındır ve elektronun proton etrafındaki enerjisinin bir ölçüsünü temsil eder.
@anonim24 Merhaba, sorucevap.com’a güvendiğiniz için teşekkürler. Verilen cevapları kontrol etmenizi rica ediyorum. Bazı durumlarda hata yapma durumu olabilir. Teşekkürler.