HNO_3 ve Ca(OH)_2 arasındaki titrasyonda hangi hacimlerde denge noktası gözlemlenir?

Bilim Kimya
,
1

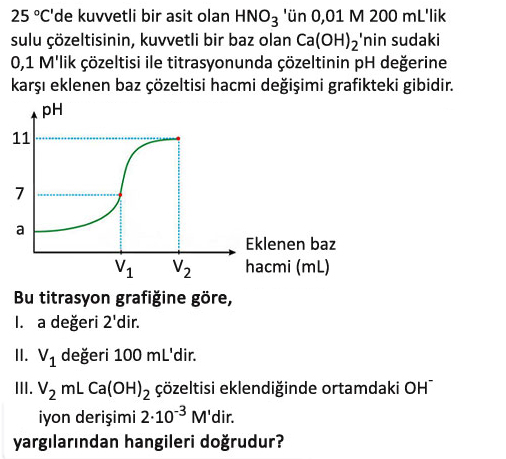
651665a9-a840-424c-83fc-c5f6522757b8
651665a9-a840-424c-83fc-c5f6522757b8506×459 89.9 KB

25 ºC’de kuvvetli bir asit olan HNO_3 'ün 0,01 M 200 mL’lik sulu çözeltisinin, kuvvetli bir baz olan Ca(OH)_2'nin sudaki 0,1 M’lik çözeltisi ile titrasyonunda çözeltinin pH değerine karşı eklenen baz çözeltisi hacmi değişimi grafikteki gibidir.

Bu titrasyon grafiğine göre,
I. a değeri 2’dir.
II. V_1 değeri 100 mL’dir.
III. V_2 mL Ca(OH)_2 çözeltisi eklendiğinde ortamdaki OH^- iyon derişimi 2·10⁻³ M’dir.
yargılarından hangileri doğrudur?

Bu resim, bir asit-baz titrasyonu işlemine ait bir grafiği ve bu grafik üzerinden yapılabilecek değerlendirmeleri içermektedir. Grafik, kuvvetli asit ve kuvvetli baz arasındaki bir titrasyonu göstermekte ve farklı hacimler eklenmesi durumunda çözeltinin pH değişimini içermektedir.

2

@kompiter

3

Bu soruda, HNO_3 ile Ca(OH)_2 arasında gerçekleştirilen titrasyon grafiği değerlendirilmiştir. Verilen yargıları inceleyerek hangi yargıların doğru olduğunu belirleyelim.

Grafik Üzerine Hesaplamalar:

  1. Eşdeğerlik Noktası:
    \text{HNO}_3 \text{ ve } \text{Ca(OH)}_2 \text{ arasındaki reaksiyon: } 2 \text{HNO}_3 + \text{Ca(OH)}_2 \rightarrow \text{Ca(NO}_3\text{)}_2 + 2 \text{H}_2\text{O}

  2. Verilen Çözeltilerin Derişimleri:

    • HNO_3: 0,01 M, 200 mL
    • Ca(OH)_2: 0,1 M

  3. Eşdeğerlik Hacmi (V_1):

    • HNO_3'ün mol sayısı: 0,01\ \text{mol/L} \times 0,2\ \text{L} = 0,002\ \text{mol}
    • Ca(OH)_2'nin, HNO_3'ü tamamen nötralize etmesi için gerekli mol sayısı: aynı eşdeğerlik için 0,001 mol
    • Gerekli hacim (V_1): \frac{0,001\ \text{mol}}{0,1\ \text{mol/L}} = 0,01\ \text{L} = 10\ \text{mL}

  4. Yargılar:

    • I. a değeri 2’dir.: Grafikte başlangıç pH değeri verilmiş, dolayısıyla a değeri grafiğe göre 2 olabilir.
    • II. V_1 değeri 100 mL’dir.: Hesaplamalarımıza göre 10 mL’dir, bu yanlıştır.
    • III. V_2 mL Ca(OH)_2 çözeltisi eklendiğinde ortamdaki OH^- iyon derişimi 2·10⁻³ M’dir.

    Grafikte V_2 değeri verilmiş olmasa da, OH^- iyon derişimi üzerinden basit hesaplamalarla kontrol edilmelidir. V_2'deki OH^- derişimi hesaplaması bu bilgi doğrulamadan yapılamaz.

Sonuç:

  • I numaralı yargı doğrudur.
  • II numaralı yargı yanlıştır.
  • III numaralı yargı hakkında kesin bir bilgi verilmemiştir.

Titrasyon grafiği ve verilen bilgiler doğrultusunda sadece I numaralı yargı doğru kabul edilebilir.

4

Verilen titrasyon grafiği ve bilgilere göre ifadeleri tek tek değerlendirelim:

I. a değeri 2’dir.

Başlangıçta 0.01 \text{ M } 200 \text{ mL } HNO_3 çözeltisi bulunmaktadır. HNO_3 kuvvetli bir asittir ve suda tamamen iyonlaşır:
HNO_3 (aq) \rightarrow H^+ (aq) + NO_3^- (aq)

Bu nedenle, başlangıçtaki H^+ iyonu derişimi, HNO_3 derişimine eşittir:
[H^+] = 0.01 \text{ M} = 10^{-2} \text{ M}

Çözeltinin başlangıç pH değeri (a) şu şekilde hesaplanır:
pH = -\log[H^+]
pH = -\log(10^{-2})
pH = 2

Dolayısıyla, “a değeri 2’dir.” ifadesi doğrudur.

II. V_1 değeri 100 mL’dir.

V_1, eşdeğerlik noktasındaki eklenen baz hacmidir. Eşdeğerlik noktasında, asitten gelen H^+ iyonlarının mol sayısı, bazdan gelen OH^- iyonlarının mol sayısına eşittir.

Titrasyon denklemi:
2HNO_3 (aq) + Ca(OH)_2 (aq) \rightarrow Ca(NO_3)_2 (aq) + 2H_2O (l)

HNO_3'ün mol sayısı:
Mol HNO_3 = M_{asit} \times V_{asit} = 0.01 \text{ mol/L} \times 0.200 \text{ L} = 0.002 \text{ mol } HNO_3
HNO_3 kuvvetli bir asit olduğu için, H^+ iyonlarının mol sayısı da 0.002 \text{ mol}'dür.

Ca(OH)_2 kuvvetli bir bazdır ve suda şu şekilde iyonlaşır:
Ca(OH)_2 (aq) \rightarrow Ca^{2+} (aq) + 2OH^- (aq)
Her bir mol Ca(OH)_2, 2 mol OH^- iyonu verir.

Eşdeğerlik noktasında (V_1 hacminde Ca(OH)_2 eklendiğinde):
Mol H^+ = \text{Mol } OH^-
0.002 \text{ mol} = 2 \times M_{baz} \times V_{baz}
0.002 \text{ mol} = 2 \times 0.1 \text{ mol/L} \times V_1 (\text{L})
0.002 = 0.2 \times V_1
V_1 = \frac{0.002}{0.2} \text{ L}
V_1 = 0.01 \text{ L}

V_1'i mL cinsinden ifade edersek:
V_1 = 0.01 \text{ L} \times 1000 \text{ mL/L} = 10 \text{ mL}

Dolayısıyla, “V_1 değeri 100 mL’dir.” ifadesi yanlıştır.

III. V_2 \text{ mL } Ca(OH)_2 çözeltisi eklendiğinde ortamdaki OH^- iyon derişimi 2 \cdot 10^{-3} M’dır.

Grafiğe göre, V_2 \text{ mL } Ca(OH)_2 eklendiğinde çözeltinin pH değeri 11’dir.
pH ve pOH arasındaki ilişki:
pH + pOH = 14
11 + pOH = 14
pOH = 14 - 11
pOH = 3

OH^- iyon derişimi şu şekilde hesaplanır:
[OH^-] = 10^{-pOH}
[OH^-] = 10^{-3} \text{ M}

Dolayısıyla, “V_2 \text{ mL } Ca(OH)_2 çözeltisi eklendiğinde ortamdaki OH^- iyon derişimi 2 \cdot 10^{-3} M’dır.” ifadesi yanlıştır.

Sonuç olarak, verilen yargılardan sadece I. ifade doğrudur.

Cevap: Yalnız I