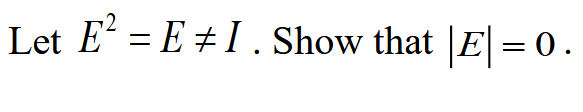Linear Cebir Proof

Eğitim ve Öğretim Matematik
,
1

image
image583×112 4.66 KB

Let E^2 = E \neq I . Show that |E| = 0 .

2

  1. İdempotent Matris:
    E^2 = E denkleminden, E matrisinin idempotent bir matris olduğu anlaşılır. Yani bir matrisi kendisiyle çarptığınızda yine kendisini verir.

  2. Eigenvalues:
    İdempotent matrislerin özdeğerleri (eigenvalues) yalnızca 0 veya 1 olabilir. Bunu şöyle açıklayabiliriz:

    • Eğer \lambda, E matrisinin bir özdeğeri ise, o zaman:
    E\mathbf{v} = \lambda \mathbf{v}

    eşitliğini sağlayan sıfırdan farklı bir \mathbf{v} vektörü vardır.

    • E^2 ye bakarsak:
      E^2 \mathbf{v} = E(\lambda \mathbf{v}) = \lambda (E\mathbf{v}) = \lambda^2 \mathbf{v}
      olur. Fakat E^2 = E olduğu için:
      E^2 \mathbf{v} = E \mathbf{v} = \lambda \mathbf{v}
      eşitliklerinden, \lambda^2 = \lambda elde ederiz. Bu da \lambda (\lambda - 1) = 0 anlamına gelir, dolayısıyla \lambda = 0 veya \lambda = 1.

  3. Determinant:
    E \neq I olduğu için tüm özdeğerler 1 olamaz. En az bir özdeğer 0 olmak zorundadır. Bu, |E| = 0 sonucunu verir çünkü bir matrisin determinantı, özdeğerlerinin çarpımıdır ve çarpanlardan biri 0 olduğunda sonuç 0 olur.

Bu adımlarla, |E| = 0 olduğunu göstermiş olduk.