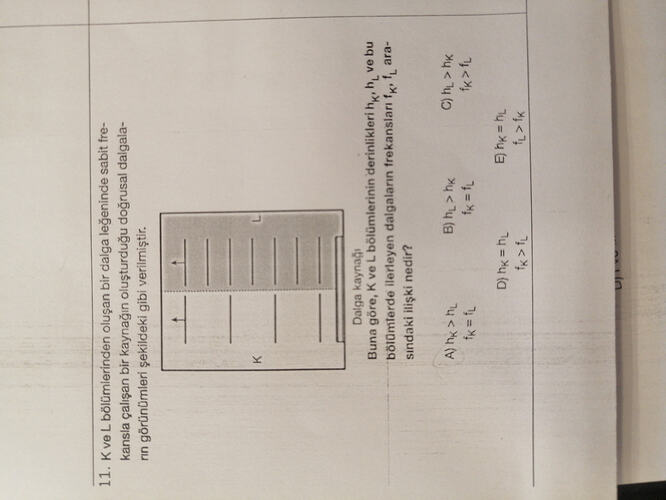
- K ve L bölümlerinden oluşan bir dalga leğeninde sabit frekansla çalışan bir kaynağın oluşturduğu doğrusal dalgaların görünümü şekildeki gibi verilmiştir.
[Şekil içinde yazılar]
L
K
Dalga kaynağı … Buna göre, K ve L bölümlerinin derinlikleri h_K, h_L ve bu bölümlerde ilerleyen dalgaların frekansları f_K, f_L arasındaki ilişki nedir?
A) h_K > h_L
f_K = f_L
B) h_L > h_K
f_K = f_L
C) h_L > h_K
f_K > f_L
D) h_K = h_L
f_K > f_L
E) h_K = h_L
f_K < f_L
Özet: Soru, sabit frekansta çalışan bir dalga kaynağının K ve L olarak iki bölümden oluşan dalga leğeninde oluşturduğu doğrusal dalgaların görünümüne bakarak derinlikler h_K, h_L ile frekanslar f_K, f_L arasındaki ilişkiyi sorgulayan çoktan seçmeli bir fizik sorusudur.
Bu soruda kullanılan dil Türkçe, ben de Türkçe devam edeceğim.
Önce soruyu metin hâline getireyim, sonra çözümü yazacağım:
Resimde, K ve L bölümlerinden oluşan bir dalga leğeninde sabit frekansla çalışan bir kaynakla oluşturulmuş doğrusal dalgaların görünümü verilmiş. K kısmında dalga boyları L kısmına göre daha seyrek (yani \lambda_K > \lambda_L). Metnin yan kısmında (okunabildiği kadarıyla) bölmelerin derinlikleri h_K ve h_L, bu bölümlerde ilerleyen dalgaların frekansları f_K, f_L arasındaki ilişki soruluyor.
Kaynak aynı olduğuna göre dalgaların frekansı leğenin her yerinde aynıdır:
f_K = f_L
Suda dalga hızı v, ortamın derinliğine bağlıdır: derinlik arttıkça su dalgasının hızı artar. Ayrıca
v = \lambda \cdot f
olduğundan, frekans sabitken dalga boyu büyük olan yerde hız da büyüktür.
Resimde K kısmındaki dalga boyu, L kısmındaki dalga boyundan büyüktür:
\lambda_K > \lambda_L
Dolayısıyla
v_K > v_L
hızın büyük olduğu yerde derinlik de daha fazladır, yani
h_K > h_L
Sonuçta:
- Derinlik ilişkisi: h_K > h_L
- Frekans ilişkisi: f_K = f_L
Şıklara göre doğru kombinasyon h_K > h_L ve f_K = f_L olan seçenektir.