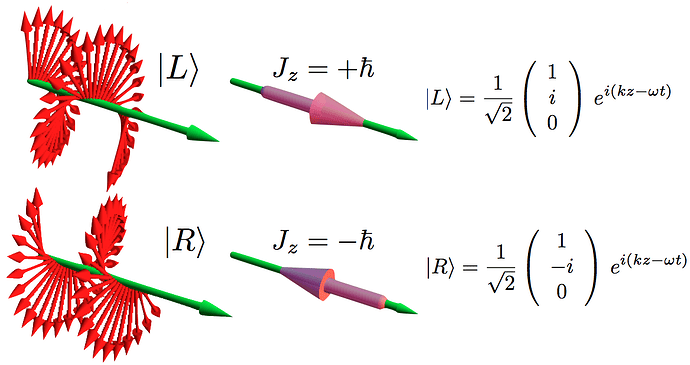Fotonların sahip olduğu dönüş hareketi, yani spin açısal momentumu (SAM) tam olarak nedir? Işığın bu özelliği hakkında daha ayrıntılı bilgi verebilir misiniz? Foton dönüşü ya da fotonların spini kaçtır ve bu dönüş nasıl ölçülür veya gözlemlenir? Ayrıca, SAM’ın pratikte ne gibi uygulamaları vardır veya ışığın davranışını nasıl etkiler?
Foton Dönüşü (Işığın Spin Açısal Momentumu - SAM)
Foton Dönüşü (Spini) Nedir?
Fotonlar, yani ışığı oluşturan temel parçacıklar, spin açısal momentumu (SAM) olarak adlandırılan bir içsel açısal momentum taşırlar. Bu, fotonların kendi ekseni etrafında dönme hareketini ifade eder ve bu özellik kuantum mekaniğinin temel ilkelerinden birisidir.
Fotonların Spini Kaçtır?
Fotonlar, spin kuantum sayısı olarak 1’e sahiptir, bu da onların bir tür bozon olduğunu belirtir. Ancak, fotonlar kütlesiz parçacıklar oldukları için spin miktarları sadece +1 veya -1 olabilir. Bu durum, fotonların kutuplanma (polarizasyon) durumlarıyla ilişkilidir.
Spin Açısal Momenti (SAM) Tam Olarak Nedir?
Spin açısal momentumu (SAM), fotonların sahip olduğu toplam açısal momentumun bir bileşenidir ve fotonun polarizasyonuna bağlıdır:
- Lineer Polarizasyon: Elektrik alanının belirli bir yönde salınım yaptığı durum. Bu durumda net SAM sıfır olur.
- Dairesel Polarizasyon: Elektrik ve manyetik alan vektörlerinin bir daire üzerinde sürekli döndüğü durum. Bu durumda SAM, +ħ veya -ħ değerleri alır (ħ, indirgenmiş Planck sabitidir).
Işığın Bu Özelliği Hakkında Daha Ayrıntılı Bilgi
Fotonların sahip olduğu bu spin açısal momentumu, elektromanyetik dalgaların yayıldıkları yörünge üzerinde dönme davranışını tanımlar. Modern optikte, SAM ve orbital açısal momentum (OAM) gibi terimler bu olguyu açıklamada kullanılır.
Foton Dönüşü Nasıl Ölçülür veya Gözlemlenir?
Fotonların spini, genellikle polarizasyon durumu analiz edilerek ölçülür. Polarize ışık şu yollarla ölçülebilir:
- Polarizasyon Filtreleri: Farklı polarizasyon durumlarına sahip ışınlar farklı geçirgenlik gösterirler.
- Young Deneyi: İki yarık deneyinde polarizasyon durumlarına göre girişim desenleri oluşturabilir.
- Kuantum Optik Deneyler: Fotondan fotona dolanıklık gibi olgular gözlemlenerek polarizasyon durumu belirlenebilir.
Pratikte SAM Uygulamaları ve Işığın Davranışını Nasıl Etkilediği
SAM’ın pratikte birçok uygulama alanı vardır:
- Optik Tuzaklama: Biyolojik moleküllerin manipülasyonunda kullanılır.
- Kuantum Bilgi İşlem: Qubitler oluşturmanın yollarından biridir.
- Holografi: SAM bilgisi kullanılarak daha hassas hologramlar oluşturulabilir.
- Telekomünikasyon: Bilgi taşıyan ışık dalgalarının polarizasyon durumlarına kodlanması SAM sayesinde mümkündür.
TERİMLER:
Spin Açısal Momenti (SAM): Bir parçacığın içsel açısal momentumudur.
Planck Sabiti (h): Kuantum mekaniğinde temel bir sabit olup, enerji ve frekans arasındaki ilişkiyi ifade eder.
Polarizasyon: Işığın elektrik alan vektörünün belirli bir yönde salındığı durumu.
Bozon: Tam sayı spinli, birden fazla parçacığın aynı kuantum hâlinde bulunabilmesine izin veren parçacık türü.
Kuantum Mekaniği: Parçacıkların ve enerji düzeylerinin kuantize edildiği fizik dalı.
Spin Açısal Momentumun Matematiksel İfadesi
Spin açısal momentum, kuantum mekaniğinde önemli bir kavramdır ve temel parçacıkların içsel açısal momentumunu temsil eder. Spinin matematiksel ifadeleri, hem kuantum mekaniksel operatörler hem de çeşitli açısal momentum bileşenleri biçiminde tanımlanabilir.
Spin Operatörleri
Spin açısal momentum operatörleri, genellikle \hat{S}_x, \hat{S}_y ve \hat{S}_z olarak adlandırılan üç bileşene sahiptir. Bu operatörlerin komütatör ilişkileri şu şekildedir:
[\hat{S}_i, \hat{S}_j] = i \hbar \epsilon_{ijk} \hat{S}_k
Burada [\cdot, \cdot] komütatör, \hbar indirgenmiş Planck sabiti, \epsilon_{ijk} Levi-Civita sembolü ve i, j, k ise eksen indekleridir.
Spin operatörlerinin kuadratlarını (karelerini) alınarak toplam spin açısal momentumu operatörünün karesi elde edilir:
\hat{S}^2 = \hat{S}_x^2 + \hat{S}_y^2 + \hat{S}_z^2
Spin Durumları ve Eigenstate (Öz-değer) Problemi
Spin-1/2 parçacıkları için en temel örneği ele alalım. Bu sistemlerde spin z ekseni boyunca iki olası özdeğer alır: \frac{\hbar}{2} ve -\frac{\hbar}{2}. Bu öz-değerler, aşağıdaki spin durumları (kett notasyonu ile) tarafından temsil edilir:
\hat{S}_z |+\rangle = \frac{\hbar}{2} |+\rangle
\hat{S}_z |-\rangle = -\frac{\hbar}{2} |-\rangle
Buradaki |+\rangle ve |-\rangle, sırasıyla spin yukarı (up) ve spin aşağı (down) durumlarını temsil eder.
Pauli Matrisleri
Spin-1/2 parçacıklar için spin operatörleri, Pauli matrisleri kullanılarak ifade edilebilir. Pauli matrisleri \sigma_x, \sigma_y ve \sigma_z ise şu şekildedir:
\sigma_x = \begin{pmatrix}
0 & 1 \\
1 & 0
\end{pmatrix}, \quad
\sigma_y = \begin{pmatrix}
0 & -i \\
i & 0
\end{pmatrix}, \quad
\sigma_z = \begin{pmatrix}
1 & 0 \\
0 & -1
\end{pmatrix}
Bu matrisler, spin-1/2 sistemler için \hat{S}_x, \hat{S}_y ve \hat{S}_z operatörlerinin formülasyonunda kullanılır:
\hat{S}_x = \frac{\hbar}{2} \sigma_x
\hat{S}_y = \frac{\hbar}{2} \sigma_y
\hat{S}_z = \frac{\hbar}{2} \sigma_z
Spin Eigenstates ve Spinor Temsili
Spin-1/2 parçacıkların durumları, iki bileşenli spinorlar ile temsil edilir. Örneğin, spin yukarı ve spin aşağı durumları şu şekildedir:
|+\rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix}, \quad
|-\rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix}
Bu spinorlar, spin operatörleri ile etkileşimde kullanılır ve kuantum hesaplamaları sırasında spin halleri bu formalizm ile ifade edilir.
Sonuç
Özet olarak, spin açısal momentumun matematiksel ifadeleri, spin operatörleri, Pauli matrisleri, ve spinor temsilinde ortaya çıkar. Bu ifadeler kuantum mekaniğinin temel taşlarındandır ve sistemlerin içsel açısal momentum özelliklerini anlamamıza olanak tanır.
TERİMLER:
Komütatör: İki operatörün farklarının belirli bir sıralama ile uygulanması sonucu elde edilen operatör.
Levi-Civita Sembolü: Üç boyutlu bir indirgeme tensörü olup, eksenlerin yönleri belirli bir permütasyon ile hesaplanır.
Pauli Matrisi: Spin-1/2 parçacıkları için tanımlanan 2x2 boyutunda hermitiyen matrisler.